角的8字模型
此模型因外形像数字8,故名为"8字"模型.初中几何8字模型是几何题中最常见的的模型之一,常用于推导角、边之间的关系以及证明三角形相似.
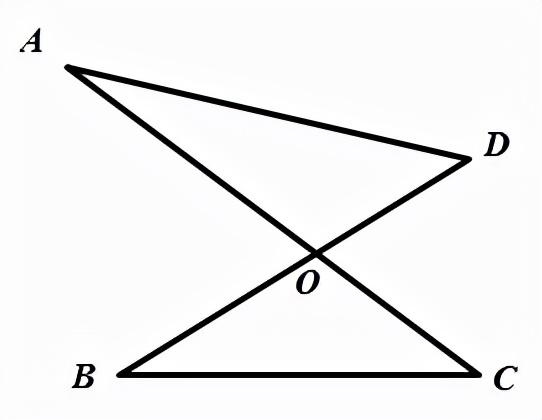
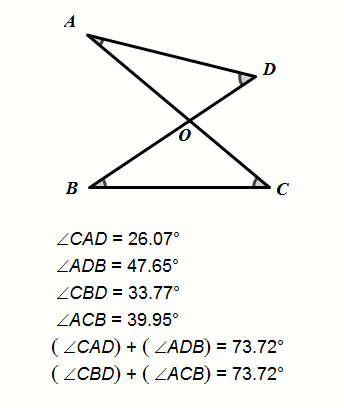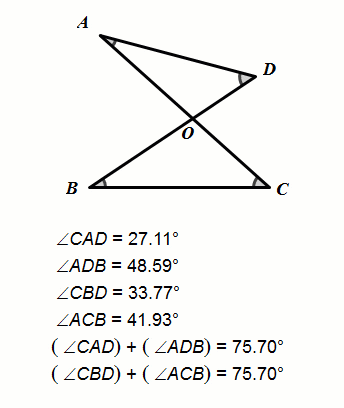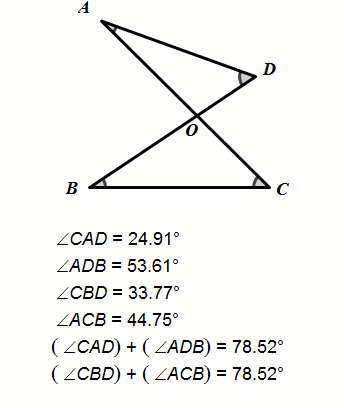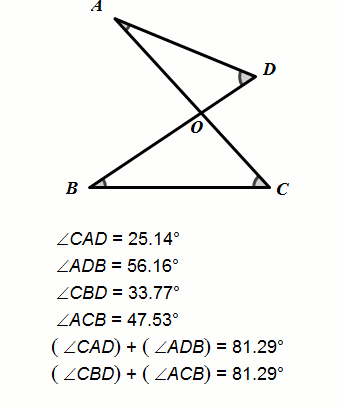
结论:∠A+∠D=∠B+∠C.
动态几何验证
推理证明
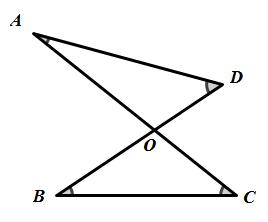
证法一:
如上图,
∵∠AOB是△AOD、△BOC的外角,
∴∠AOB=∠A+∠D,
∠AOB=∠B+∠C.
∴∠A+∠D=∠B+∠C.
证法二:
如上图,
∵∠A+∠D+∠AOD=180°,(三角形内角和为180°)
∴∠A+∠D=180°-∠AOD.
∵∠B+∠C+∠BOC=180°,(三角形内角和为180°)
∴∠B+∠C=180°-∠BOC.
∵∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C.
典例分析
观察下列图形并写出答案
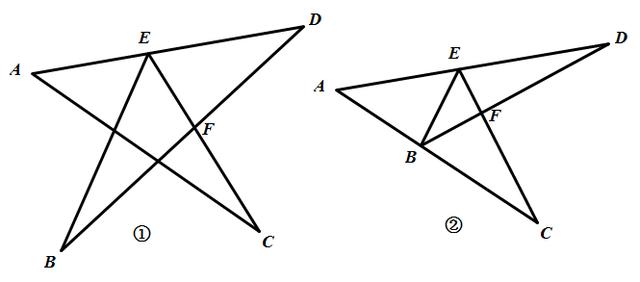
(1)如图①,∠A+∠B+∠C+∠D+∠E=_________;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F=_________;
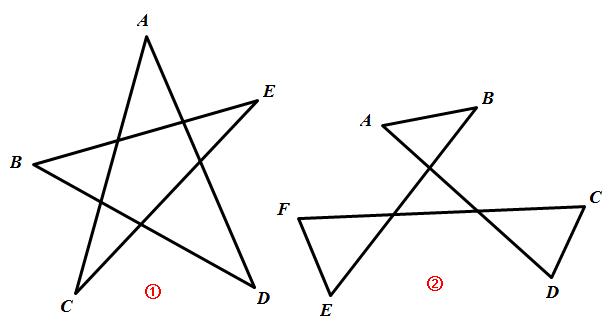
解析:
(1)解法一:利用角的8字模型.
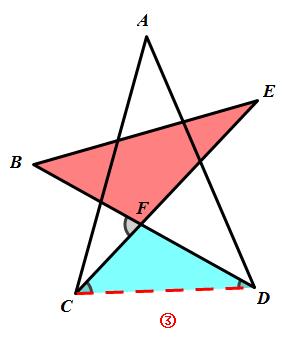
如图③,连接CD.
∵∠BFC是△BEF的外角,
∴∠B+∠E=∠BFC.
∵∠BFC是△CFD的外角,
∴∠FCD+∠FDC=∠BFC.
∴∠B+∠E=∠FCD+∠FDC.
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠FCD+∠FDC
=∠A+∠ACD+∠ADC
=180°.
解法二:如图④,利用三角形外角和定理.
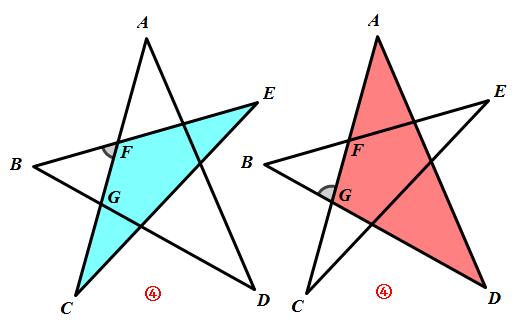
∵∠BFG是△FCE的外角,
∴∠BFG=∠C+∠E.
∵∠BGF是△AGD的外角,
∴∠BGF=∠A+∠D.
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠BFG+∠BGF
=180°.
(2)解法一:如图⑤,利用角的8字模型.
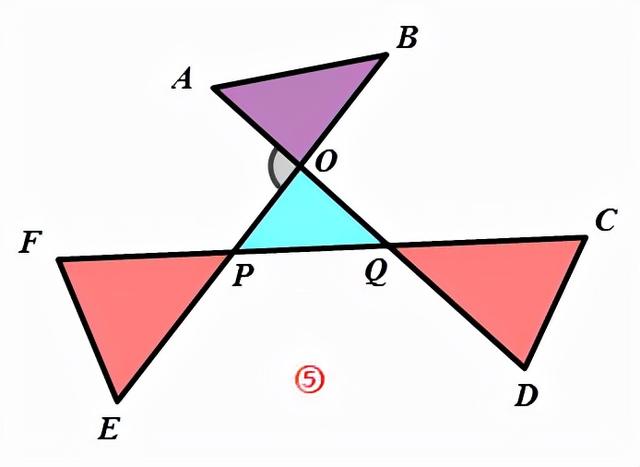
∵∠AOP是△AOB的外角,
∴∠A+∠B=∠AOP.
∵∠AOP是△OPQ的外角,
∴∠OPQ+∠OQP=∠AOP.
∴∠A+∠B=∠OPQ+∠OQP.①
同理:∠C+∠D=∠OPQ+∠POQ.②
∠E+∠F=∠POQ+∠OQP.③
联立①+②+③得
∠A+∠B+∠C+∠D+∠E+∠F
=2(∠OPQ+∠OQP+∠POQ)
=360°.
解法二:利用角的8字模型
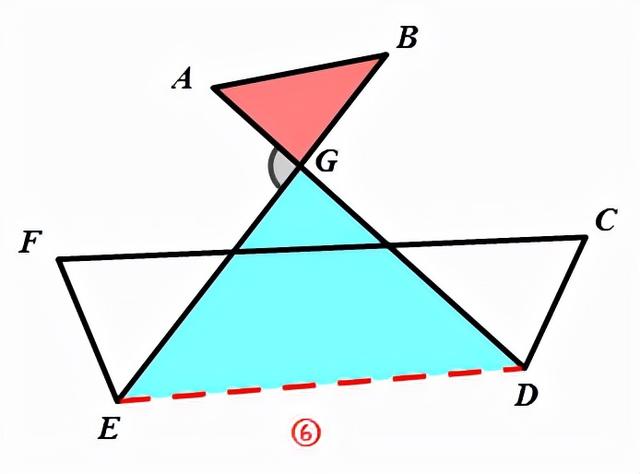
如图⑥,连接DE.
∵∠AGE是△AGB的外角,
∴∠A+∠B=∠AOE.
∵∠AGE是△GED的外角,
∴∠GED+∠GDF=∠AGE.
∴∠A+∠B=∠GED+∠GDF.
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F
=∠GED+∠GDF+∠C+∠ADC+∠FEB+∠F
=360°.
模型演练
1.(1)如图①,求:∠A+∠B+∠C+∠D+∠BEC=__________;
(2)如图②,求∠A+∠EBD+∠C+∠D+∠BEC=_________.
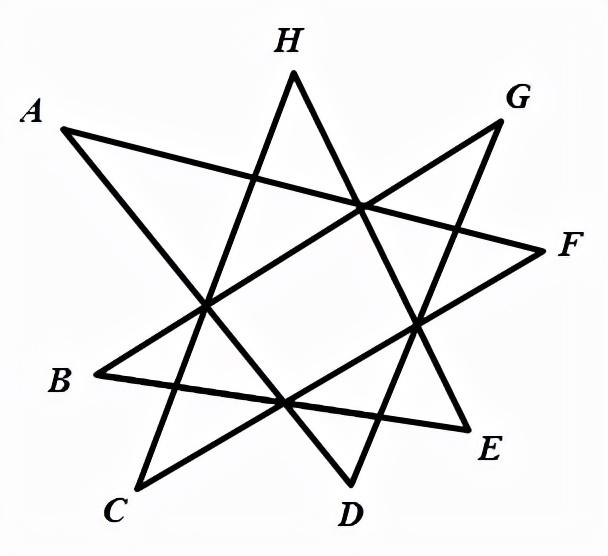
2.如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=____________;
提前引入:共圆8字模型(后期重点补充)
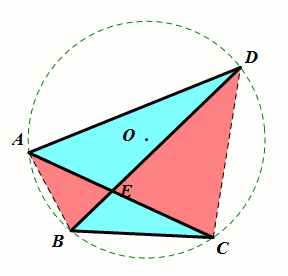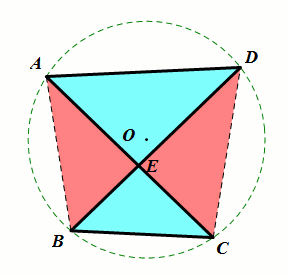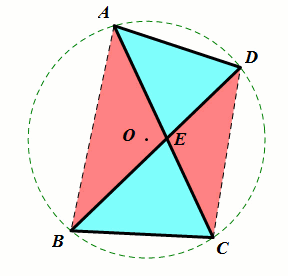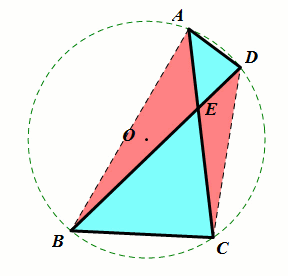
条件:当∠DAC=∠DBC(同侧一组角相等).
结论:∠D=∠C (A,B,C,D四点共圆);
ΔAED∼ΔBEC (上下相似);
ΔAEB∼ΔDEC;(左右相似).
总结:8字模型同侧一组角相等⇒另一侧也相等(后续证明:利用圆或三角形相似)
共圆+平行的“8字”模型=等腰梯形
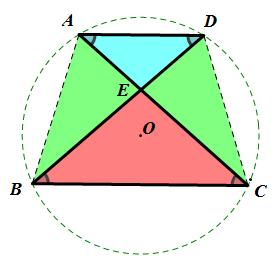
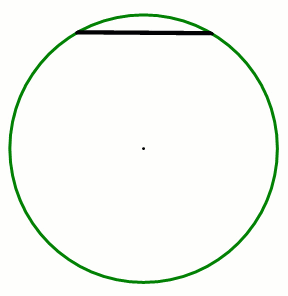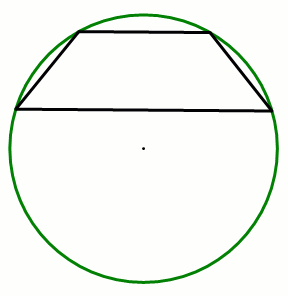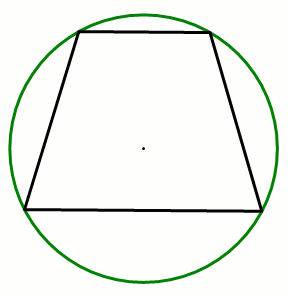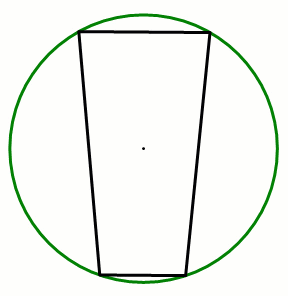
条件:A,B,C,D四点共圆,AD∥BC.
结论:四边形ABCD为等腰梯形(圆中的平行线所夹的弧相等).
总结:等腰梯形四点共圆,连接对角线可构造“8字”模型,“上下相似”(ΔAED∼ΔBEC)、“左右全等”( ΔAEB≅ΔDEC).
在初中几何学习中,要注意概念关、语言关、画图关、推理证明关四大关。善于静中找动,实现从特殊到一般的转化。动中找静,找到运动过程中不变的数学模型或规律,再从一般到特殊,利用临界情况解决问题。动静结合,其乐无穷!解决几何问题不顺手的原因是由于对基本的模型图及结论掌握不牢固,还有常见的几何解题方法不够熟练。本公众号作者潜心研究整理初中几何学习过程中常见的几何基本模型图及结论,如有错误或更好的思路,请大家不吝赐教。
你的关注与分享就是对本作者的最大支持与动力。知识在于分享,分享知识,传播正能量,让我们携手共进,共建有效的课堂教学、提升学习效果。