好多朋友在后台留言让我们复刻其中的小实验?
这不就大家安排上了

实验器材
所标杯、剪刀、镜子、双面胶、白纸、铅笔、橡皮、尺子
(硬纸板、打印机等替换器材)

实验过程
首先,我们来看一个简单的小例子
将一个特殊的纸片翻转并粘贴

我们在外面看到的是正方形
从镜子里面看到的是菱形


尝试换一个角度去观察它
就看到其中的奥妙所在

那么我们怎样去制作这样一个视错觉玩具呢?
我们可以从一张白纸,或者借助电脑的图形工具开始:
首先画出我们想要直接看到的、和想从镜子中看到的截面图形
两个图形需要是由线段组成的多边形,
且要使得两者的宽度相等
然后画一条水平线,将多边形的各个顶点投影至水平线上
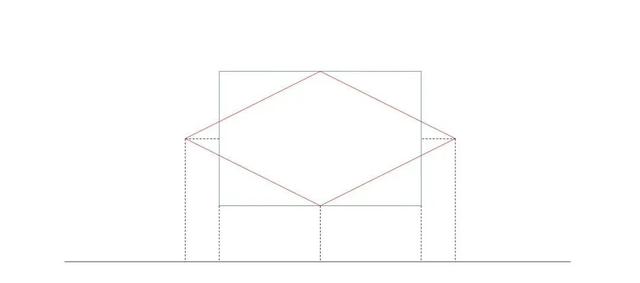
然后在每个图形顶点对应的投影处
分别画出两个方向倾斜45°的斜线
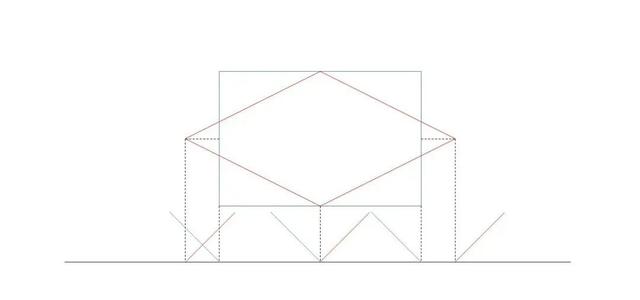
延长这些斜线来获得一些交点
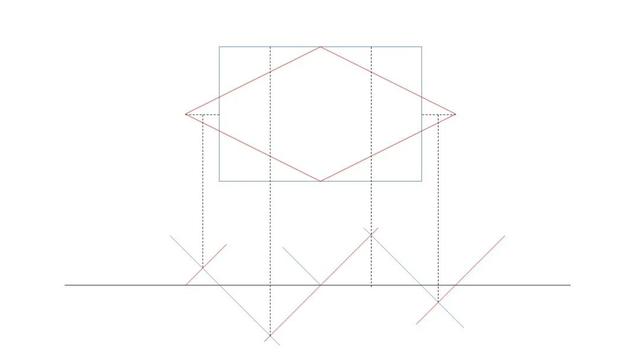
注意每个交点都是由在截面图中处在同一水平位置的点,投影处的斜线所交汇而成
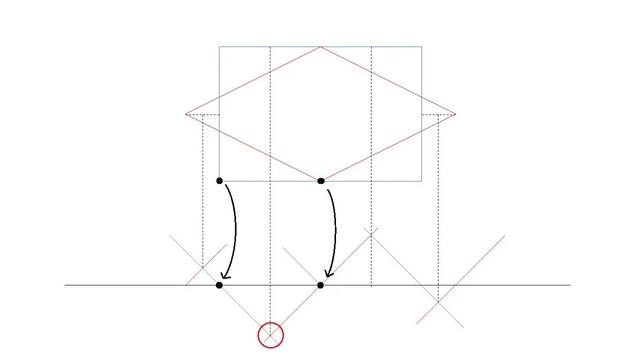
做这些交点到水平线的中垂线段,
并且做辅助线延长这些线段到截面中对应的水平高度并标点
然后连接这些标点:
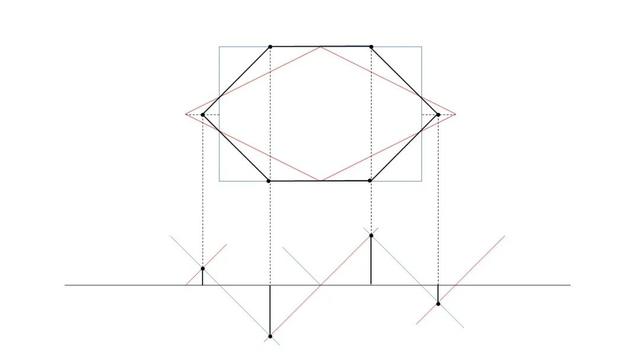
大家可以花几秒钟思考一下这组图形像什么?
对啦,上图的黑线实际上就是我们所需柱体的俯视图,
而下图是柱体的正视图~
之后我们可以借助纸、笔、尺,或者打印机
将我们的俯视图与主视图变成一张展开的轮廓图:
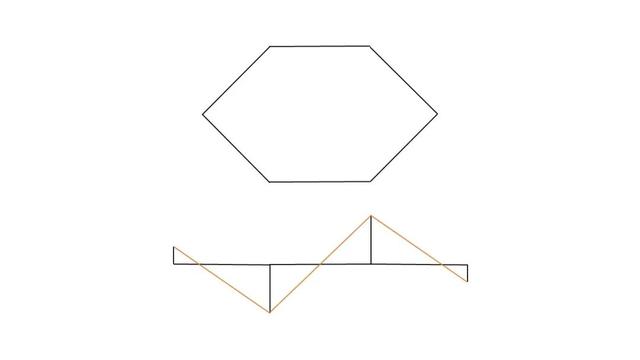
将轮廓图做一个水平对称,然后在旁边预留方便粘贴的部分,
就完成了所需柱体的完整展开图啦
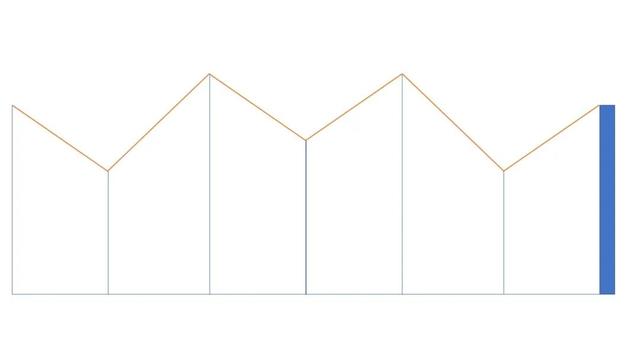
有了这个方法我们就可以创造各种我们想要的视错觉小玩具
而这其中也有更有意思的事可以发现:
比如如果我们设想一个对称性比较高的错觉图案:
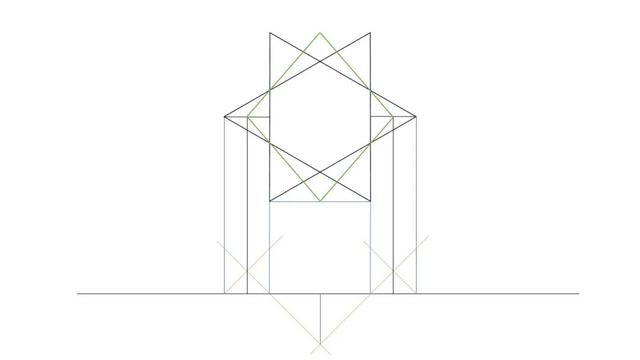
在上图中我们想从两侧观测到两个形状一样但是方向相反的三角形
如果我们对调两个三角形被观测的角度,三视图会怎样变化呢?
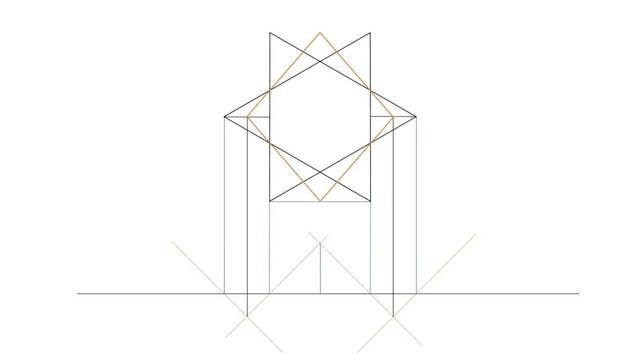
我们发现二者如此的相似,最终的展开图也是如此:
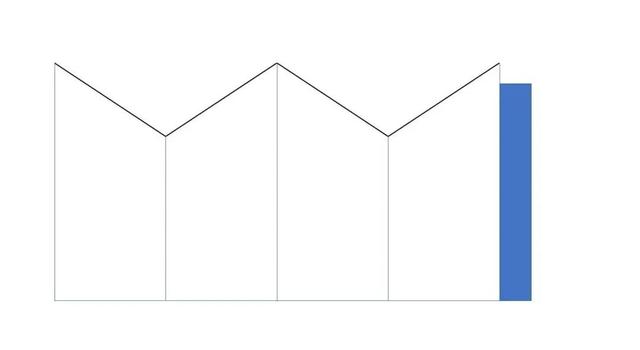
所以当我们从一个方向观测这组错觉图时,
我们看到了同向向前的两个三角形:

将它旋转90°再观察,便能看到两个同向向后的三角形

是不是很神奇呢~
原理解说
对于处在镜子同一法平面的两个点来说,我们直接观测它们和观测它们在镜子中呈的虚像时,光路图的简化版本如下:
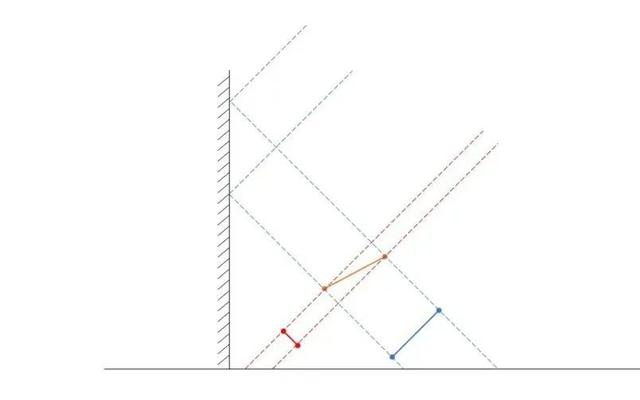
对于连接两点的边缘(橙色线段),我们从两侧看到的像的投影分别为红蓝两条线段。而当我们把这个像投影至同一水平线时,就能看出我们制作步骤的方法来源:
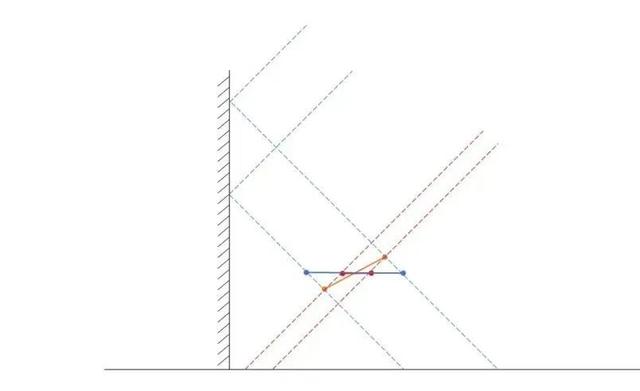
我们只需要确定每个端点的投影位置来确定柱边高度,是因为当两个像都是直边时,端点之间的相对位置是线性变化的,所以作为物的柱边也是在同一平面内的直线。这也是为什们我们在最开始推荐大家用多边形作为想要看到的像。如果想要看到带有曲边的像时,借助编程或者取多点做近似,也是可以实现的。
在以上的分析中我们做了平行光的近似,实际上我们的眼睛离物体与镜子都很近,会产生近大远小的透视效应,会使我们实际看到的图形有一些变形。这种变形可以用增加柱体的厚度来缓解,所以如果大家有硬纸板的话做出的效果应该会更好一些~
编辑:荔枝