
哥尼斯堡
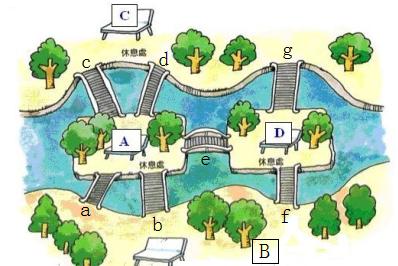
1735年,有几名大学生写信给当时正在俄罗斯的彼得斯堡科学院任职的天才数学家欧拉,请他帮忙解决一个问题:在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?
于是,欧拉1736年访问了普鲁士的哥尼斯堡小镇,这是个风光明媚、人杰地灵的好地方,一条名叫普雷格尔河的小河蜿蜒其间。这座闻名遐迩的小城,诞生了一位伟大的哲学家康德(西方哲学的扛把子)和一位大数学家希尔伯特(被誉为"数学界的无冕之王",天才中的天才)。

欧拉在亲自观察了哥尼斯堡七桥后,认真思考走法,但始终没能成功,于是他怀疑七桥问题是不是原本就无解呢?
同年,29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,在解答问题的同时,开创了数学的一个新的分支-----图论与几何拓扑。
一般来说,数学家们写论文阐述自己的成果,大多会省略其思维过程,欧拉在这个报告中,却一反常规,详细完整地叙述了自己的思维过程.这文献太珍贵了,且难以找到,既然我找到了,不敢藏私,遂贡献出来,以飨大家。论文下面的文字为笔者的注释(对论文的疑难点做注解)、解读(对论文的主旨作归纳、整理和提问)与鉴赏(通过提问的方式,总结对我们以后解题、学习的启示),就教于各位同好。小标题是笔者自己所加。
哥尼斯堡七桥问题欧拉(1736年)
想清目标在动手(1) 讨论只与位置有关,研究位置的性质的几何分支,莱布尼兹叫它“位置几何学”(现称“拓扑学”——引用者)
注释:在另外一篇文献中对开头描述的比较详细:
“讨论长短大小的几何学分支,一直被人们热心的研究着。但是还有一个至今几乎完全没有探索过的分支;莱布尼兹最先提起过它,称之为“位置的几何学”。这个几何分支讨论只与位置有关的关系,研究位置的性质;它不去考虑长短大小,也不牵涉到量的计算。但是至今未有过令人满意的东西,来刻划这门未知几何学的课题与方法……”
解读:本小节指出与问题相关的数学知识,亦即是“弄清题意”,化归数学模型——位置几何学,阐述位置几何学的特点与遗憾。确立自己的解决方法是根植在位置几何学上的新的几何——只考虑与点线的相对位置(点是否在线上,线是否通过点)有关的性质,而与图像的形状、大小无关的新的几何问题。即现代所谓的拓扑学——一门只研究图形各部分位置的相对次序的学科。
(2)问题:在普鲁士的哥尼斯堡镇,有一个岛叫“奈发夫”,普雷格尔河两支绕流其旁(图1),七座桥a,b,c,d,e,f,g横跨两支流.问,一个人能不能在一次散步中,每桥恰走一次?有人说不行,也有人怀疑,但无人坚持说一定可能;
在此基础上,我给自己提出下面这个很一般的问题:给定任意一个河道图与任意多座桥,要判断能否每桥恰走一次。
解读:明确自己具体面对的问题是什么?这个问题有一般性吗?一般性是什么?
本小节欧拉说明自己解决问题的大概思路,先把问题抽象化,再一般化。
鉴赏:
①了解你的问题,并尽量的想一想这是你所熟悉的问题吗?你能把它归类你所熟知的哪一类问题?如果没有,你能想到相近或相似的题目的吗?有没有可能借鉴它呢?你可以利用它的结果吗?你能利用它的方法吗?
② 欧拉在此提出的一般性问题符合创造者悖论:越宏大的计划,越有机会获得成功,多个问题也许要比一个问题容易回答,较全面的定理可能更容易证明,较普遍的题目可能更容易解答。当然宏大的计划不能是盲目的、自负的,而应是超越了那些表面现象的东西、洞察了题目的本质之后。
(3)“七桥”这特殊问题可这样来解:细心地把所有走法列表,逐一检查哪些(如有的话)是满足要求的、然而这解法太乏味、太烦琐了,因可能组合的数目太大,且对于桥数更多的问题便无法应用.且这样分析,会引出许多与问题无关的支节.因此,须另寻佳法,即能一下子找出满足要求的路线的方法,它会十分简单。
注释:
①想把每种方法走一遍,大概有5000多种(7!=7×6×5×4×3×2×1=5040),每天走一种,大概需要13.8年。即使不算回头路,也要走将近7年。
②这种方法就是完全归纳法,穷举所有的可能性,不重不漏是关键,可按字典排列法去执行。
③繁难则简,欧拉应该实地走过的,也可能是在“走”的时候发现了新思路。牛顿不就是被苹果砸到了而发现的“万有引力”的吗?南京大学2012年(110周年校庆)还把那棵树的“三根枝条”通过空运,不远万里引到仙林校区。
寻找好方法(简单易懂)的突破口在哪儿呢?且看下文欧拉的如何引爆思维的撞针,如何抓住问题的关节点的。如何“数学地”思考问题的?
解读:
欧拉先说这是个特殊而又具体的问题,故而可用特殊的具体的方法:每种方法都走一遍,不过时间长一些,现在用电脑模拟可以很容易用此种方法解决,但这种方法少了些思辨,少了些味道,多了些繁杂,多了些古板,多了些无趣。
但是对普通的哥尼斯堡人来说,这可能正是趣味所在,或许大家根本不想这个问题被解决,每天按不同的路线走一边未尝不是一件有意思的事情。
对于数学家来说“乏味、繁琐”,可能只是普通人每天要面对的生活,生活的意义不一定非要高大上,活着本身就是生活的全部意义所在。在数学家眼中我们就是小蚂蚁,每天无聊而又无知的活着,实际上这也挺好,就比如说我以为自己是网络中的菜鸟,实际上我可能只是个肉鸡。
辛弃疾说:我见青山多妩媚,料青山见我亦如是。这恐怕不太现实,因为数学家在我的眼中就是不可高攀的神,是疯子也是圣人。
鉴赏:
我们解决一个数学问题时,尤其是生活实际问题是,我们必须了解题目。如何了解呢?你可以试着问自己一些问题:我应该从哪里开始?我能做什么?我该做什么?我能想到什么?我了解题目吗?我熟悉题目吗?未知是什么?已知是什么?条件是什么?条件是否能满足未知量?或着它不够充分?或着多余?或着矛盾?你能否画一张图,引入适当的符号。将条件的不同部分分开,你能把它们写出来吗?
波利亚的解题表“必须理解题目”中的这段话可能就是根据欧拉的解决思路的写的,你看二者多贴合。
 智者紧盯目标
智者紧盯目标(4)方法的依据是:以适当的简易方式把过桥记录下来:以A,B,C,D表被河道分割的陆地,当一个人从A经a或b到B时,记作AB,第一字母表出发地,第二字母表到达地,如此人继续由B过桥f到D,两次过桥记作ABD,等等。
从具体到抽象是数学发展的一条重要大道——华罗庚 (1910-1985)
注释:
欧拉首先对地方和桥进行抽象:舍弃地方的大小、形状、位置,而把它看作是一个个的点;舍弃桥的形状、结构、大小抽象成一条条的直线;不考虑地方与桥是怎样连接,只考虑是否相通;舍弃过桥的具体过程、方式并加以抽象,把“过桥”用两个字母表示,前者表示“入”,后者表示“出”,把过桥的一系列过程抽象成有序的字符串,欧拉推理时看到的实际上是如下的点线图。
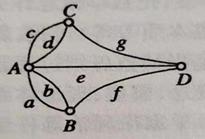
欧拉通过抽象,引入适当的数学符号,简化问题,把问题真正的数学化——找到了问题恰当的数学表征。
小贴士:
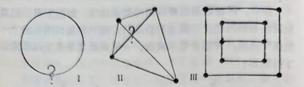
网络:指某些由点和线组成的图形,网络中的线弧都有两个端点,而且不想交。如果一个网络中的任意两点,都可以找到网络中的某些弧线,把它们连接起来,那么,这样的网络是连通的。连通的网络称为脉络。
显然,下面的三个图中,图I不是网络,因为他仅有的一条弧线只有一个端点;图II也不是网络,因为它中间的两条弧线相交,而交点不是顶点;图III是网络,但却不是连通的。
而七桥问题的图形,则不仅是网络,而且是脉络!
网络的点如果有奇数条的弧线交汇于它,这样的点称为奇点。反之,称为偶点。
(5)类似地,如此人再从D过桥g到C,则记作ABDC,就是说,此人从A出发过了三座桥到C,且必须过三桥经B,D才能到C.过四桥用五个字母表示;一个人过任意多座桥,表示路线的字母比桥数多一,如过七桥需用八个字母。
注释:
再次强调字母的顺序意义及现实意思,总结了规律:表示路线的字母个数比桥数多一。这也是解决问题的关键——“七桥问题”能否按此规律用八个字母顺序表示呢?
(6)按此法,不必区分走哪座桥,于是如有一条路走过七桥中每桥恰一次时,用八个字母表示,则在这串字母中,AB(或BA)的组合要出现两次,因有两桥连接A,B;类似地,AC这组合要出现两次,AD,BD,CD这三个组合各出现一次。
解读:
欧拉引进这套符号系统是恰当的,它可以真实的反应实际问题,去掉不相关的干扰,把“过桥”这个行为的本质都通过符号恰当的表征出来。
因此,这套符号系统真实的表征了题意,它形象而又客观的描述了题目的已知、未知和条件,从而也就完全反映了问题的结构。
小贴士:一个恰当的好的符号系统,必须与被表示的数学问题密切相关,即它的每个符号对应着问题中的概念或命题,而且它的符号的每个有意义的组合,和这些组合的推演变化,也对应着数学问题中某些事项和事项的变化,反之亦然。
如(4)(5)(6)欧拉用大写字母A、B、C、D表示河岸与小岛;则AB表示“由A出发,过桥到B”;ABC表示“由A出发,过桥到B,再过桥C”;反之“由A出发,过桥到B,再过桥D,再过桥C”可以记成ABDC.而字符串的“结构特征”(AB或BA出现几次,A出现几次,由多少字母组成等)则反应了问题的要求。
鉴赏:
解题的一个重要的步骤就是选择符号。小心的、敏锐的选择题目中需要用符号指示的那些元素,以促进我们从本质上对题目的理解。
一个好的符号必须是毫无含糊的、富有意义的、便于记忆的、易于辨认的;它应该尽量避免有害的多种含义与利用有用的多重含义;符号的次序与彼此联系必须能表明事物之间的次序和联系。
(7)于是,问题化成:怎样用四字母排成八字母串,使(6)中提到的各二字组合出现所需次数.然而,在致力寻求这样的排列之前,对其可能的存在性在理论上稍作考虑,是必要的,因为若它不存在,则去求它等于白费力气.所以,我就致力于去寻求一个简易判别排法是否存在的法则.
注释:
在明确“七桥问题”就是“八字符串中两字母组合出现规定次数”的问题的基础上,提出“这样的排列是否存在”的问题。
此段说了两个问题:
首先是问题的转化,解决问题实际上就是不断地对问题转化的过程,一直转化到我们熟知的概念、常识、结论、定理等等上面,这中间需要设置一个个的“中途点”,“八字符串中两字母组合出现规定次数”就是这样的中途点。
其次,设置的中途点是否合情合理,是否有解更是关键。这就告诉我们在解题的过程中不可以盲目的向前,要及时的回头看看它的合理性、可行性,需要作调整吗?怎样调整?

我们的人生之路不也正是如此吗!
(8)为此,考虑地区A,设有桥a,b,c,d,…与之相通(图2)、先看桥a,如步行者过此桥,他必定过桥之前或之后在A.

按上述记法,A定出现一次;如有3桥通A,三桥中每桥过1次,则无论是否从A出发,则A必定出现2次.如5桥通A,则A出现3次;如桥有奇数座,则加1取半,其商即为A出现的次数.
注释:
①欧拉注意到,对于网络中的某个点,如果不是开始点(起点)或者结束点(终点),那么它若有一条弧线进来,必有另一条弧线出去。也就是说交汇于这样点弧线必定成双成对,即这样的点必定是偶点。
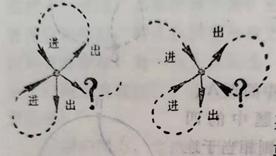
②因为①的原因,欧拉在此只讨论奇点的情况,有进必有出,故而“如桥有奇数座,则加1取半,其商即为A出现的次数”就很容易理解了。
③为了弄清楚“符号要求的八字母串”的结构规律,欧拉找到了字母出现次数与通过该处桥数的具体关系,至此“七桥问题”的解决可以说已经水到渠成。
(9)回到七桥问题(图1),因有5桥a,b,c,d,e通A,则在路线表示式里A必出现3次;有3桥通B,则B应出现2次,类似地,D,C各出现2次;就是说,在过桥路线的八字母串里,必有3个A,2个B,2个C,2个D,这是不可能的,因此,按所说方式走遍这七座桥是办不到的.
注释:
至此“七桥问题”圆满解决,结束不过意味着新的开始,为了进一步弄清楚一般的河——桥系统中的“过桥”问题,寻求正面的、普遍性的解决手段,欧拉继续向前。争取找到一个结论,一个可以轻松解决此类问题的一般性结论。
如何由特殊到一般哪?尝试,再尝试——同一手段用了两次就是方法。

鉴赏:
①你能检验的你的结论吗?你能检验你的论证过程嘛?你用到了题目的所以条件了吗?你的结论适应的范围是什么?你了解它的局限性吗?
②你能用不同的方式来叙述它吗?你能重新解构你的已知、未知、论证过程吗?你能重组你解构的已知、未知、论证过程吗?
③你能推广你的结论吗?以便让它在更大的、更广的范围内使用。
未完待续,请关注@庄子的那条鱼









