“8”字模型与飞镖模型的应用非常广泛,熟练掌握其重要结论,可以使我们做题事半功倍!
模型一:“8”字模型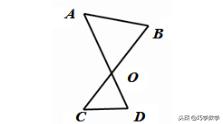
1、角的结论:∠A+∠B=∠C+∠D
2、边的结论:AD+BC>AB+CD
"8"字模型应用
练习1、(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
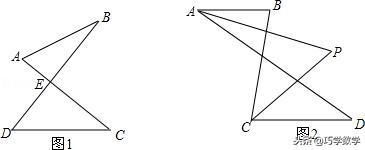
(2)如图2,AB∥CD,AP、CP分别平分∠BAD、∠BCD,
①图2中共有 个“8字形”;
②若∠ABC=80°,∠ADC=38°,求∠P的度数;
(提醒:解决此问题你可以利用图1的结论或用其他方法)
③猜想图2中∠P与∠B+∠D的数量关系,并说明理由.
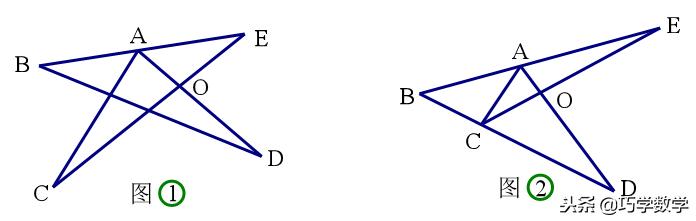
练习2、(1)如图①,求∠CAD+∠B+∠C+∠D+∠E= ;
(2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E= 。
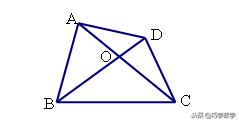
练习3:如图,四边形ABCD的对角线AC、BD相交于点O。
求证:(1)AB+BC+CD+AD>AC+BD;
(2)AB+BC+CD+AD<2AC+2BD.
 模型二:飞镖模型
模型二:飞镖模型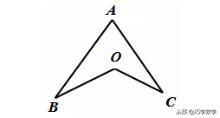
角的结论: ∠BOC=∠A+∠B+∠C
边的结论:AB+AC>BD+CD。
飞镖模型应用
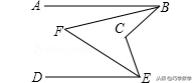
练习1、如图,已知AB∥DE,BF,EF分别平分∠ABC与∠CED交于点F,探索∠BFE与∠BCE之间的数量关系,并证明你的结论.
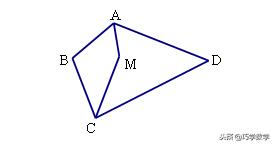
练习2、如图,在四边形ABCD中,AM、CM分别平分∠DAB和∠DCB,AM与CM交于M。探究∠AMC与∠B、∠D间的数量关系。
热搜精练
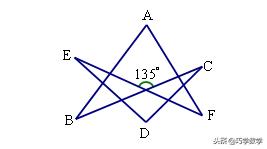
1.如图,求∠A+∠B+∠C+∠D+∠E+∠F= ;
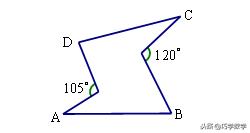
2.如图,求∠A+∠B+∠C+∠D = 。
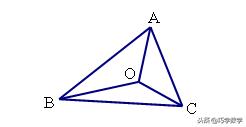
3.如图,点O为三角形内部一点。
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO.
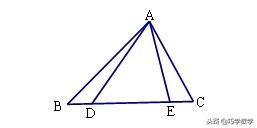
4.如图,在△ABC中,D、E在BC边上,且BD=CE。
求证:AB+AC>AD+AE。
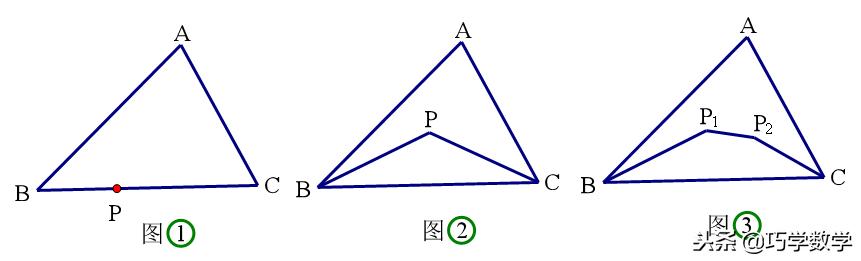
5.观察图形并探究下列各问题,写出你所观察得到的结论,并说明理由。
(1)如图①,△ABC中,P为边BC上一点,请比较BP+PC与AB+AC的大小,并说明理由;
(2)如图②,将(1)中的点P移至△ABC内,请比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)图③将(2)中的点P变为P1、P2,请比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由。