欢迎来到 "走进高维空间系列 "的第五部分,在这里我们将探索高维空间的一些奇怪和反直觉的奇观。距离高维空间系列第四部分:”走进高维空间——概率论与高维空间的深层次联系“已经有一年多了。在阅读第五部分之前,我建议先浏览以下前四部分内容。
简单回顾以下前四部分的内容:
第一部分我们得出:在无限维空间中球体的体积都集中在边界上,我们只能知道这个结论,但是无法想象!第二部分的结论是,在高维空间中,内切于球内的立方体不完全在球体以内。.在第三部分中,我们推导出,在无限维空间中,点与点之间的距离都是相等的。第四部分讨论的是高维空间与概率论的联系。这些疯狂的、无法想象的高维空间现象让人兴奋,我们只能借助数学等工具去理解它们的真正含义。这篇文章,我们将见证这些奇迹之一是如何影响一个广泛使用的统计工具的。让我们开始吧!
预测问题在各种领域中,人们通常会根据一个或多个预测变量的值来预测某个响应变量的值。也许我们希望预测一个病人在出院后30天内再次入院的概率(响应),因为有各种人口统计学和临床特征(预测因素例如,年龄、是否有并发症、实验室测量)。或者,我们希望根据房屋的各种特征(如邻里关系、卧室数量、面积)来预测房屋的销售价格。或者我们希望根据各种环境和农业特征(如降雨量、土壤成分、害虫管理策略)预测作物产量。
可靠地预测某些响应变量的值的能力是非常强大的,有大量的方法可以解决这类问题,每种方法都有不同的优点和局限性。今天,我们将特别关注其中的一个方法,因为它非常直观,最重要的是,它给我们提供了一个观察高维空间的一些奇迹的机会。
K-近邻算法(K-Nearest Neighbors)如果我们想用一组特定的预测值来预测一个新的数据点的响应值,我们只需查看训练数据,找到所有具有完全相同的预测值的数据点,并计算出对这些训练数据点观察到的响应值的平均值或中位数。问题是,我们通常没有如此丰富的训练数据,而且很少有跨越所有可能的预测值组合的训练数据。当我们想预测一个新的数据点的响应值时,我们可能有一些类似的训练数据点的响应值,但没有完全相同的预测值组合。那该怎么办呢?构建一个模型。
为预测-响应关系建模的一种方法被称为K-近邻算法。为了理解这种方法,让我们把预测变量看作是代表一些高维的预测空间。也许你想知道这意味着什么,但这其实很简单,如果我们正在处理番茄作物数据,也许在第一轴(即维度)上有总降雨量,第二轴上有土壤硝酸盐水平,第三轴上有土壤pH值,第四轴上有平均温度,等等。因此,我们的每一个数据点都代表了高维空间中的一个点,它在该空间中的坐标取决于它对每个预测变量的值。例如,让我们看一下三维作物预测空间中的几个点。
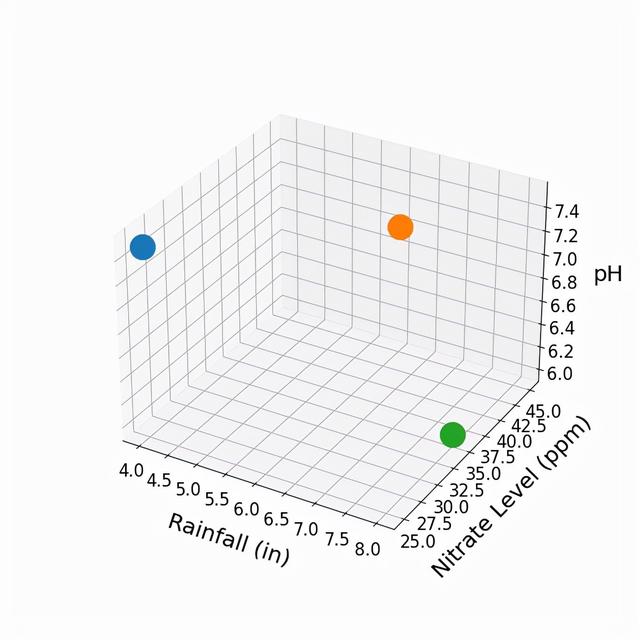
这里,绿色的点代表降雨量为8、土壤硝酸盐含量为35、pH值为6的作物;蓝色的点代表降雨量为4、土壤硝酸盐含量为25、pH值为7.5的作物;而橙色的点代表降雨量为6、土壤硝酸盐含量为45、pH值为7的作物。假设我们知道与这些西红柿作物中的每一种相关的作物产量。
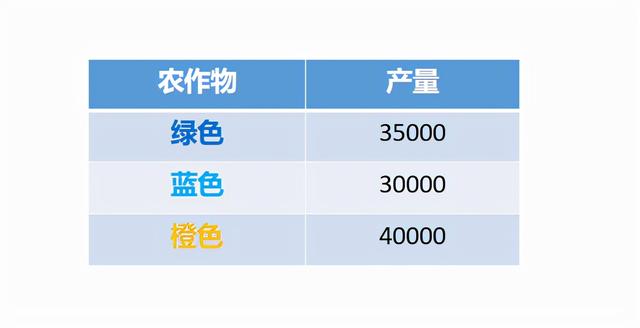
通常情况下,我们会将产量(即响应变量)作为一个额外的轴/维度进行可视化,但我在这里没有这样做,因为我们只能将三个维度可视化化。
比方说,现在是春天,我们正在种植新的西红柿作物。我们有土壤的硝酸盐水平和pH值,而且我们对预期的降雨量有一个很好的概念。我们把这个新作物表示为下面的红点。
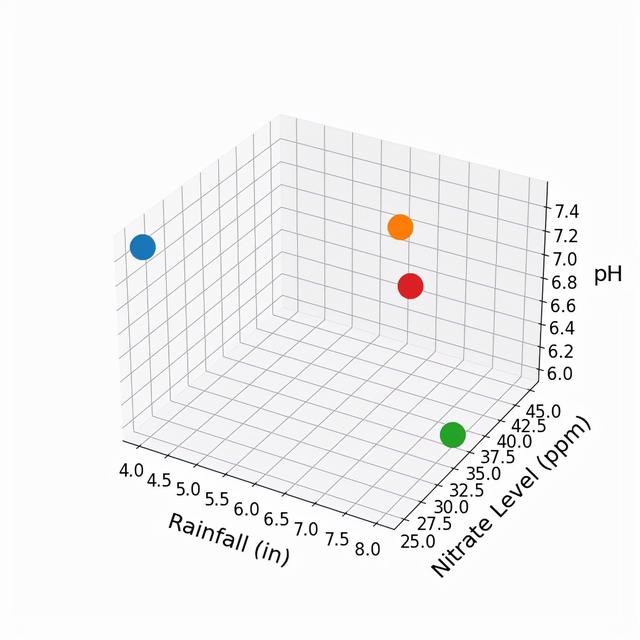
利用原来三个点的作物特性和产量,我们如何估计新的红色点的产量?有一种方法,叫做(单)近邻法,就是用原来三个点中最接近的作物产量来估计。我们会期望最近的点有大致相似的降雨量和土壤成分。看起来橙色点离红色点最近(产量为40000)。然而,从一个数据点推导出估计,不觉得有点不靠谱吗?也许与橙点相关的产量是一个意外,同样的特性在其他年份产生的产量可能会低得多。只有3个数据点,没有什么操作空间,但如果有数百个数据点呢?
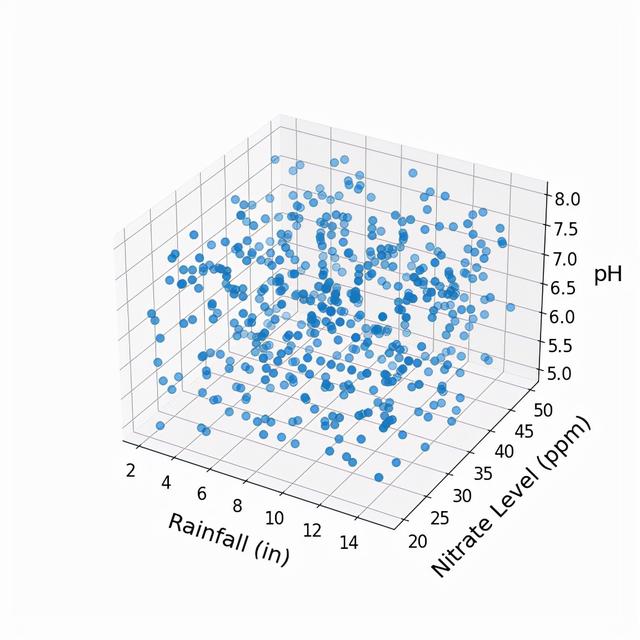
现在,加入红点所代表的新作物。
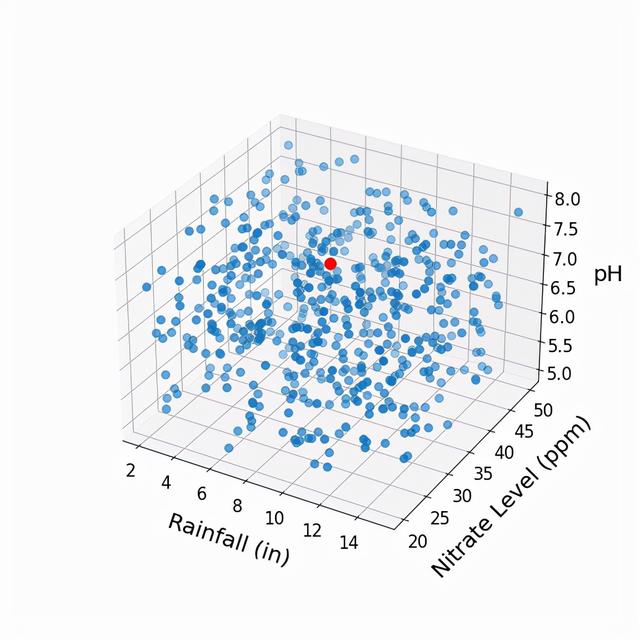
同样,我假设我们知道所有蓝点的作物产量,并希望利用这些信息来估计红点的作物产量。我们是否应该再次采用K-近邻算法? 下面,我们找出离红点最近的20个“邻居”。
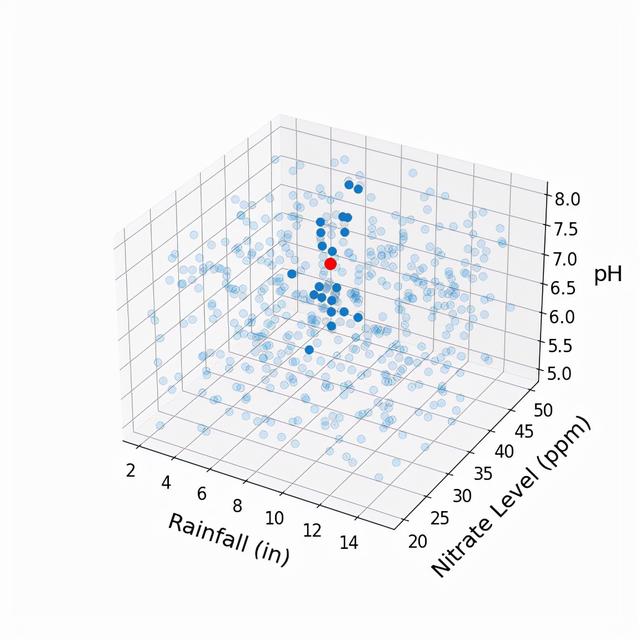
为了估计红点的作物产量,取这20个近邻的作物产量的平均值似乎很合理,对吗?在这个例子中,我们只是在三维空间中运算,但这个方法可以推广到任何维度。
我们如何定义 "最近的"?普通的欧几里得距离?还是像马氏距离( Mahalanobis distance )这样更细微的东西(它包含了不同预测因子之间的变化和关系)?这些问题都很重要(而且超级有趣),但答案与我们现在所要讨论的无关,所以我将把它们放在以后的文章中。
让我们继续向前进:高维空间!
邻居们,你们好!在接下来的部分中,我们将从有趣的应用实例(例如病人、家庭、农作物)中“撤退”,进入一个简化的空间。想象一下,我们正在处理只有一个预测变量和一个响应变量的数据;因此,预测空间只有一个维度。我们还可以想象,预测变量的值是沿着预测变量的范围均匀分布的。为了简单起见,我们使用一个只能在-0.5和0.5之间取值的预测器,这样,预测器的范围是一个单位长度。
同样,假设我们有一组数据点的预测值和响应值(称为训练数据点,因为这些是用来训练K-近邻模型的点)。让我们用蓝色来说明这些训练数据点。
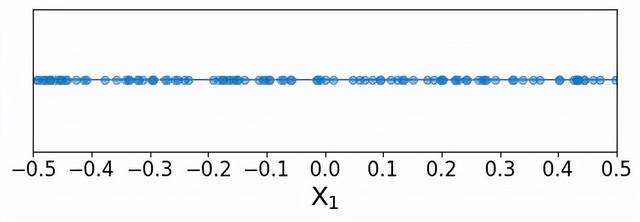
我们可以看到,训练点似乎是沿着单一预测器的所有可能值均匀分布的。现在,我们要预测一个新的点(称为索引点)的响应值,下面用红色表示。
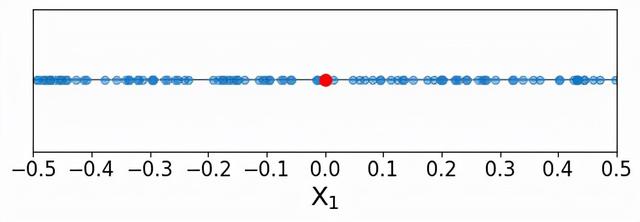
正如我们上面所学到的,K-近邻算法的一般想法是确定在预测器空间中与索引点最接近的训练数据点,然后利用这些训练点的响应值来估计索引点的响应值。重要的是,我们只使用预测器空间中靠近的训练点来为估值提供信息。如果使用在预测空间中很远的训练数据点,那么它们可能不能很好地代表索引点的响应值,而我们的最终估计值可能与事实相差甚远。
在这个例子中,假设使用最接近索引点的10%的训练数据点,从索引点出发,需要在预测器空间中达到多远才能捕获10%的训练数据?更具体地说,需要在邻域中包括多大比例的预测值范围?
单预测器的情况实际上很简单。因为训练数据点是沿着单一维度均匀分布的,而预测器的范围是[-0.5,0.5],为了捕获10%的训练数据点,只需要包含预测器范围的10%。如下图所示:
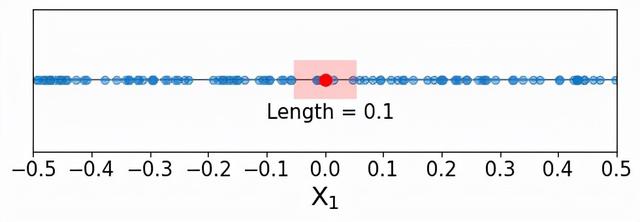
看上去很合理,对吗?我们不需要离索引点太远,就可以把10%的训练数据纳入,只需要在两个方向上取0.05个单位。目前看起来没什么特别,也许还有点无聊。让我们看看当入一个更高的维度时会发生什么。
邻居的秘密假设我们有两个预测器,每个预测器的范围是-0.5到0.5,训练数据点沿两个维度均匀分布。
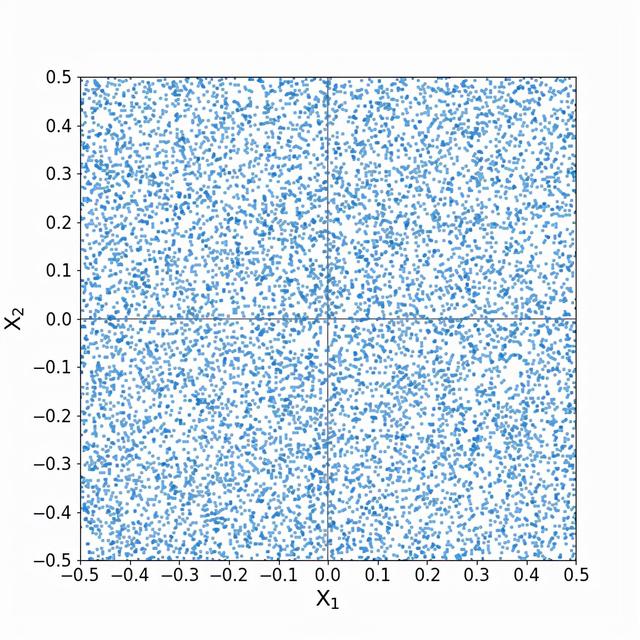
这是我们的索引点:
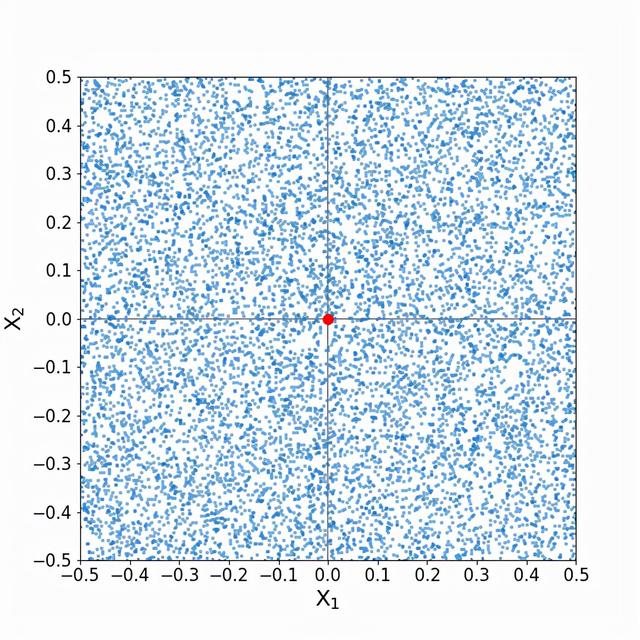
同样,我们希望捕捉10%的训练数据点。要做到这一点,每个预测器的范围中必须包括多少比例的邻居?也许我们可以把上面看到的扩展一个维度,我们将需要第一个预测器的10%和第二个预测器的10%。让我们来看看(我把训练点淡化了一些,以便更好地观察):
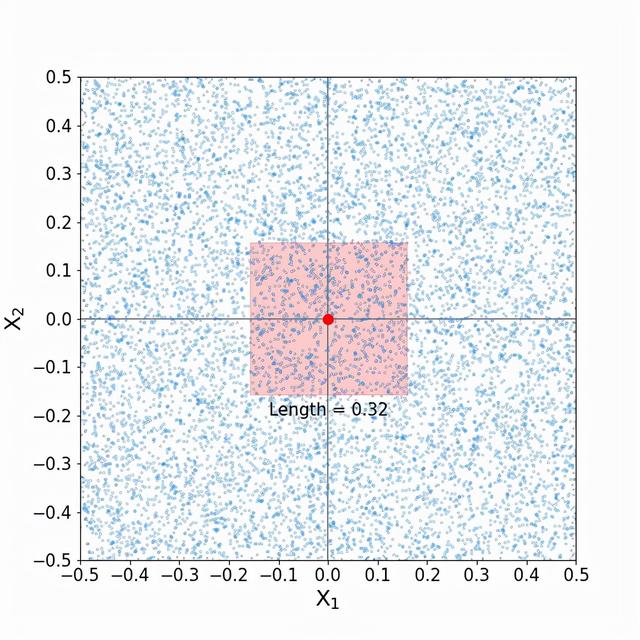
这是高维空间的奥秘中的另一个转折点!在单维空间中,我们只需要在索引空间的任何一个方向上取0.05个单位就可以捕获10%的训练数据。而现在,我们似乎必须从索引点的任何一个方向取0.16个单位,才能捕获10%的训练数据!就其预测值而言,邻域外围的训练点真的与索引点那么相似吗?答案最终将取决于数据的性质,但必须承认,当我们的目标是包括预测值与索引点尽可能相似的点时,包括每个预测器的近三分之一的范围似乎有点宽泛了。
我们继续,向三维预测器空间迈进! 下面是我们沿三个维度均匀分布的训练数据点云(左),以及索引点(右)。
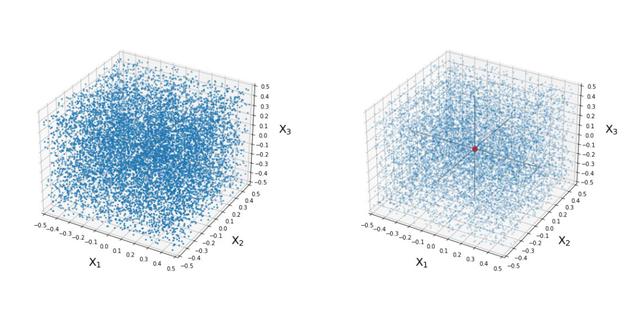
也许你已经知答案,但我再次提出问题:为了获得10%的训练点,应该怎样取值?
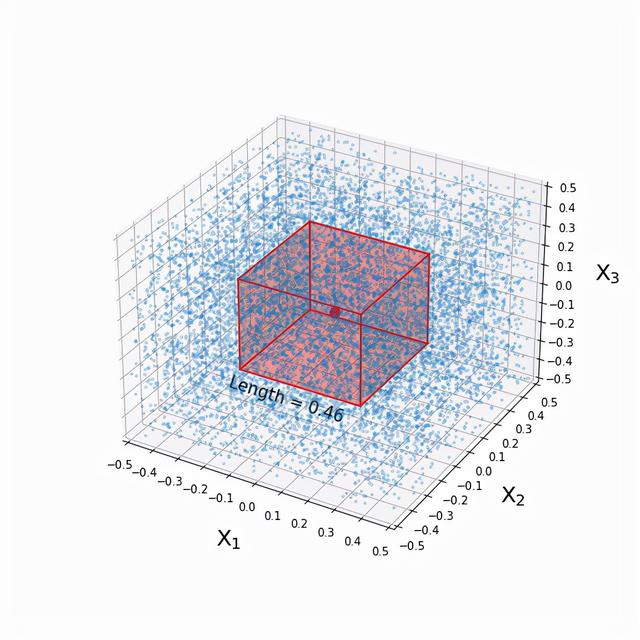
将近50%! 让我们消化一下:
在单维中,只需要包括单个预测器范围的10%,就可以定义一个包括10%的均匀分布的训练数据的邻居。在两个维度上,需要两个预测器的范围各占32%。在三个维度上,需要三个预测器范围中的每一个的46%!这里的基础数学其实很简单,真正的精彩在最后。
让我们用一个例子来说明这个问题吧,记得农作作物例子吗? pH值的范围是0-14。如果我索引点的pH值为7,那么就要在一个维度上包括pH值为6.25-7.75的训练点(直觉上似乎是合理的,对吗?),在两个维度上包括4.6-9.4(这合理吗?),在三个维度上包括3.55-10.45(这似乎开始离谱了)。将这些点称为邻居还有意义吗?
延伸在应用统计学中,使用几十个、几百个、甚至几千个预测因子是很常见的。如果在三个维度中,每个预测器的范围有近50%是用来捕捉10%的训练数据的,那么在10个维度中呢?100个维度呢?
下面的图对1到100个维度之间的每一个维度回答了这个问题。具体来说,我们把维度(即预测器)的数量放在X轴上,把每个预测器的范围比例(捕获10%的训练数据所需)放在Y轴上。
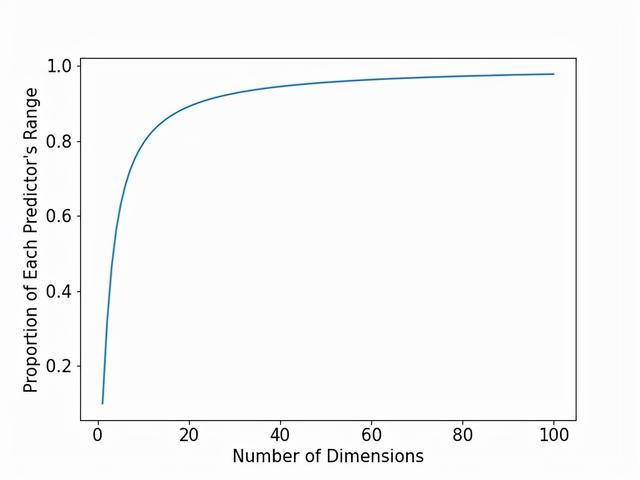
在图的最左边,我们看到了在一维、二维和三维方面的情况。然而,当达到10个维度时,几乎需要每个预测器的80%的范围!在50个维度时,需要95%的预测器范围。 到了100个维度,需要98%!
我们的目标是确定那些预测值与索引点尽可能相似的训练点。在这些更高的维度上,几乎把预测器的任何值的点视为邻居,并将使用它们来估计索引点的响应值。在我们设计的具有均匀分布的预测因子的例子中,应用K-近邻算法在一个维度上似乎是完全合理的,但在更高的维度上很快就会变得离谱。真实的数据集不会和我们探索的数据集一模一样,但这种需要进一步深入预测器空间来寻找附近点的想法依然存在。
所有的邻居都去哪儿了?让我们来探讨一个稍微不同的问题。之前,我们调查了在每个维度上取多少范围才能捕获10%的训练数据。现在,让我们看看,如果把邻居的边界限制在每个预测器范围的10%,能找到多少个邻居。在K-近邻算法的背景下,在空间上与索引点接近的训练点似乎很适合为索引点的响应值的估计提供信息。在一个维度上,一个包括10%的单一预测者范围的邻域包含了10%的训练数据。在更高的维度上会发生什么?让我们来看看。
下面的图在X轴上显示了从1到10的维度,在Y轴上显示了覆盖每个预测器范围的10%的邻域所捕获的训练数据的比例。
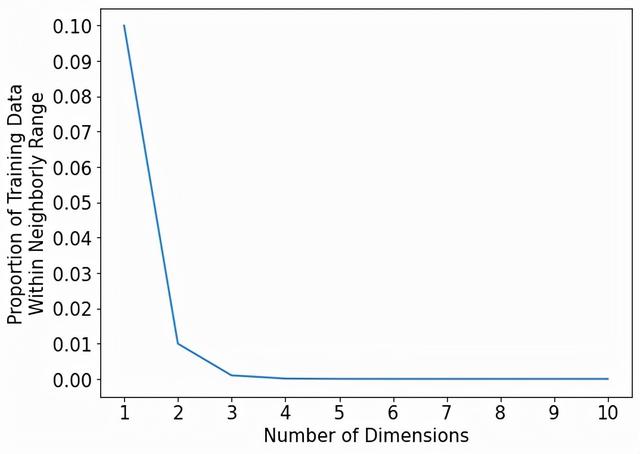
所有的邻居都去哪了?同样,在一个维度上,邻域覆盖了10%的训练数据。在二维,只有1%的训练数据! 如果我们把一个索引点的邻域定义为覆盖每个预测者范围的10%,那么一个10维的邻域将只包括训练数据的0.00000001%。
让我们用训练数据点的实际数量来重新定义这些数字,而不是百分比和比例。比方说,有100,000个训练数据点。这意味着,10维邻域平均来说,甚至没有捕捉到一个数据点(它将捕捉到0.0001个数据点)。这意味着,平均而言,每一万个邻域中,我们只能捕捉到一个邻域!这意味着很多空的邻域。这就是大量的空邻居!
因此,用一个直观合理的邻域大小(覆盖每个预测因子范围的10%),在更高维度上基本上没有邻域。而这里只到了10维!如果是100维,100万维呢?
你已经进入了一个新的领域。进入了没有邻居的地方! 邻居们都去哪儿了?为什么这些空间如此空旷?这些都是贯穿于高维空间的永恒的问题,这些问题引起了(并困扰着)许多统计学家,被精致地称为维度诅咒!
总结我们在高维空间旅程到此结束。我们不仅亲身体验了这些空间的孤独,而且还看到了这种孤独是如何影响一个著名的统计工具,著名的K-近邻算法的。
我们再一次看到,高维空间充满了神秘和惊奇。在舒适的低维物理现实中认为理所当然的特征在高维空间中变得无法辨认。
`