大家好,今天我们来聊四维,五维,六维,这样高维度空间到底是什么样子的?

提到这个话题的时候,可能有人会说,所谓的四维空间,它就是由一个三维空间加一个一维的时间所组成的概念。
其实如果这样理解的话,这完全就是一个误区。
所谓的高维度空间,它并没有时间的参与,仅仅只是空间内的概念。今天我们所聊到的话题也只是代表空间理论。

那么我们应该如何定义空间的维度呢?
所谓的三维空间,四维空间,五维空间,它们是怎么来的?我们应该怎样理解?在这里给大家举一个特别简单的方法,就是过一个点可以作几条相互垂直的直线,那么这个空间就是几维空间。

例如零维空间。过零维空间内的一个点,无法作出直线,所以它被定义为零维空间。
一维空间是一条直线,过这条直线上选择任意一个点,那么只能做一条直线,所以它被定义为一维空间。

二维空间是一个面,在这个面上可以任意选择一个点。只能做两条相互垂直的直线。

三维空间是一个立体结构,在这个空间内部任意地选择一个点,它可以构成三条相互垂直的直线。所以它也被定义为三维空间,我们可以把这三条相互垂直的直线分别给它标为x轴,y轴,z轴。

以此类推,大家想一下四维空间是什么样子的?
四维空间一定是,选择一个点,可以做四条相互垂直的直线。按照我们现有的物理空间感知,来想象这个四维空间的话。是完全无法模拟出这样的画面,似乎在这个世界上根本就不存在四条相互垂直的直线。
但是我们却可以画出四维空间在三维空间内的投影。一个三维空间的立体结构,我们很轻易的就可以画出来。
而如果把一个四维空间投射到三维空间的投影,所画出来的图像应该就是这个样子。
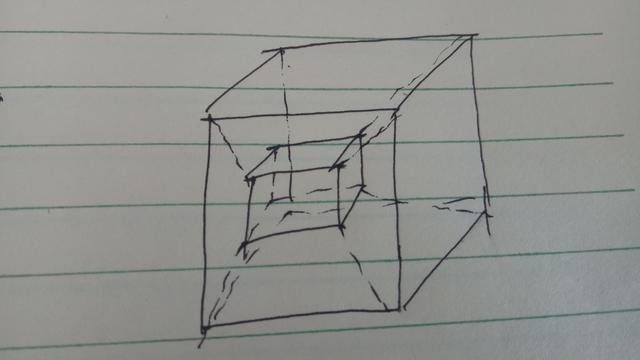
先画出一个大的立方体,然后在大的立方体内部再画一个小的立方体,最后把大立方体和小立方体的每个点连接起来。
在大立方体上选择任意一个点,我们可以看出,过这个点有四条相互垂直的直线。这四条直线按照三维空间的认知来看待的话,它们是不会垂直的。
但是假设有那么一个空间,它可以构成四条相互垂直的直线。在这里可能有人会说,明明这不是垂直的四条线,为什么非要说是垂直的?

大家切记,这只是一个四维空间在我们三维空间所构成的一个假想投影图。按照这样的思路,我们继续推理,那么五维空间,六维空间,七维空间,它们也就是分别由五条相互垂直的直线组成,六条相互垂直的直线以及七条相互垂直的直线所构成的空间。

那么说到这里,大家可能会发现,从四维空间开始往后的高维空间已经超出了我们现在的物理定律,所以我们今天所提到的四维,五维,六维这些高维度空间,它们并不是一个物理概念,而是由一个数学模型所推导出来的高维度理论。
并不能,用现有的物理认知去看待,所以它也不会违背我们现在的宇宙空间。在所有的这些维度空间内部,我们现在引入一个新的物理概念,它就是空间距离。

在零维空间内,任意两个点的空间距离。永远是零。

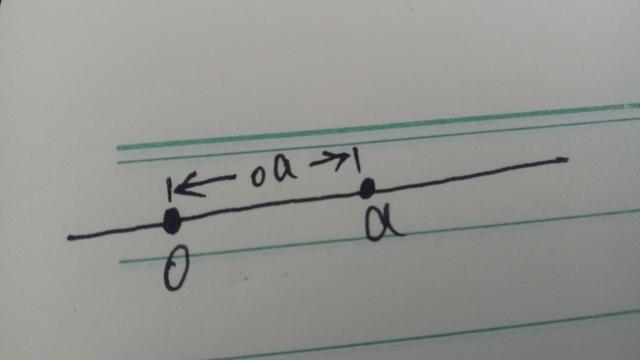
一维空间内在一条直线,选择一个点为原点。建一个横向的坐标,而任意再选择另外一个点到这个圆点的空间距离,就是这个坐标的绝对值。
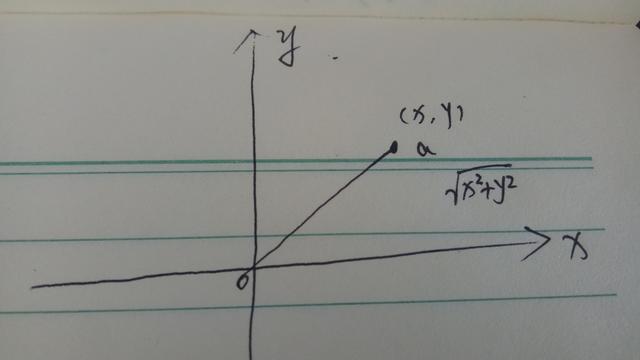
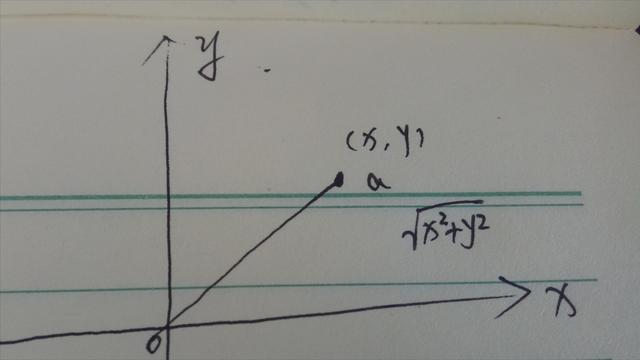
在二维空间内选择一个点为原点,分别建立x轴和y轴,那么再选择任意一个点到原点的空间距离,我们根据勾股定理就可以得出这段距离的值为根号下x方加y方。
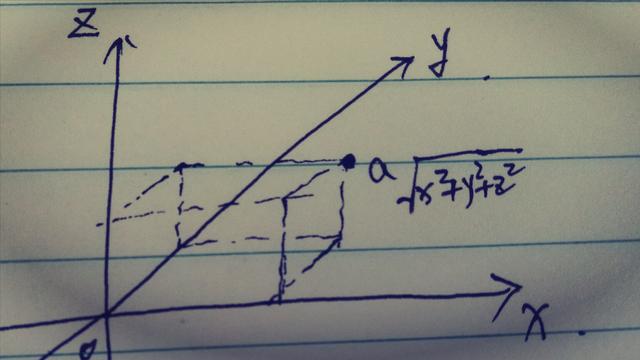
同理,在三维空间内,我们同样也可以选择一个点为原点,建立x轴,y轴和z轴。那么在这个三维空间内的任意一个点到原点的空间距离我们同样也可以得出是根号下x方加y方加z方。
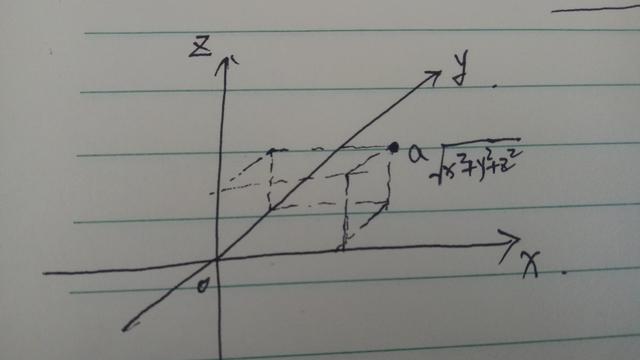
以此类推在四维空间建立坐标轴。四条相互垂直的直线分别是x轴,y轴,z轴和m轴。任意一点到原点的坐标同样也是根号下x方,加y方加z方加m方。
为什么在这里我们会提到空间距离这个概念呢?那是因为空间距离,无论我们怎样改变参考系,最后这一段空间距离,它永远是会保持不变的。
举一个简单的例子,在一维的空间,我们可以把原点放到这里,同样也可以把原点挪到其他任意一个地方,但是无论再怎么挪动原点0的位置,oa这一段的距离,它是永远不会发生改变的。
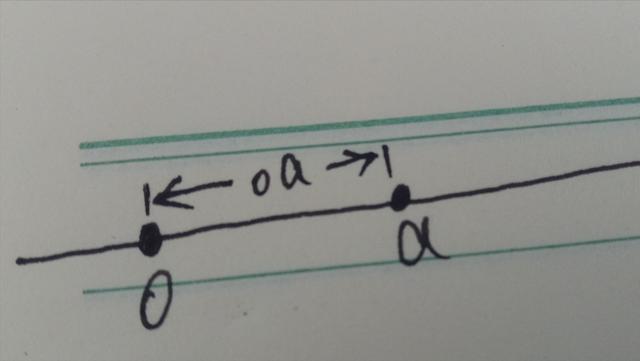
在二维空间内,我们可以这样建立坐标系,同样也可以斜着建立坐标系,但是无论怎样建立坐标系,即使a的坐标发生了变化,那么oa这一段距离,它永远是会保持不变的。这就是任意一个维度中空间距离的不变性。
在所有的维度空间中,还有一个最关键的共性。所有高维度空间它们都可以投影到低维度空间。
例如,一维空间是一条线,我们在这条线上随意的切一刀,就可以得到一个零维的点。

二维空间是一个面,在这个面上我们随意的切一刀,那么就可以得到一条一维的直线。

三维空间是一个立体结构,在这个立体结构上随意地切一刀,我们就可以得到一个二维的面。这个面切出来可以是矩形,也可以是三角形。
以此类推,我们可以得出所谓的四维空间,如果切一刀的话,它就可能得到一个三维的立体空间。
所以说了这么多高维的空间,已经超出了我们现有的物理认知,我们不能用物理的定律去看待高维的空间,而只能用数学模型抽象的去推导。

也可能我们是高维度空间的人类被降维打击了以后,进入到三维空间,所以我们现有的三维认知根本无法理解高维度空间是什么样子的?