在税务方面,统计学似乎确实有用。仔细想一想,不仅是税务,在其他众多领域都有统计学知识的应用。例如,很典型的应该就是占卜。不过,不管是西方的占星术,还是东方的生辰八字,似乎都是基于算命对象提供的生日信息,推测当事人今后的命理。生日和企业的财务报表一样都是由数字构成的,这也就意味着我们可以透过数字窥破自己命运的走向,我理解的应该没错吧?
比如,有时我们会惊讶地发现:“这两个人的生日是同一天啊!”好像因为这个巧合两个人的命运就有了必然的联系一样。我猜想在统计学领域,或者说就概率论而言,这也应当具有某种很重要的意义吧,毕竟这种情况在日常生活中并不常见
生日悖论
每个人都有生日,我们偶尔会遇到与自己同一天过生日的人,这时,你应该会自然而然地产生一种亲近感吧。但是,果真是天意如此,让你们有缘出生在同一天吗?抛开这些浪漫的幻想,我在这里还是要大煞风景地说,让我们科学地计算一下概率再来回答吧。
那么,问题来了:
在某个班级里一共有 23 名学生。不考虑双胞胎、闰年等特殊情况,在这些男孩女孩中间,有 2 个人生日相同的概率是多少?
如果在班级里发现某个同学和自己生日是同一天,一般人还是会感到些许惊讶吧。毕竟除了闰年以外,一年中有365 天,而偏偏两个人都出生在了同一天,就算是偶然,但要说没有一丝缘分的话似乎也说不过去。也就是说,在我们的直觉中,两人生日相同的概率应该是非常小的,这种缘分似乎并不常见。
但是,数学与生活又开了个玩笑,你认为不太可能的缘分,实际发生的概率要高达50.7%。

我们错了吗?这真不是一种特殊的缘分吗?
如果样本的人数增加,还会有更惊人的结果。比如30 人的话概率是70.6%,40 人的话概率是89.1%,而人数达到50 时,这个概率更是上升到了97%。反之,如果减少统计的人数,比如,减少到20人时,生日相同的比例有所下降,但也有41.1%,10 人的情况下也有11.7%。这个数据就意味着,走在东京这样的大城市街道上,和你有着同一天生日缘分的人,应该满大街都是了。
为了让大家获得更直观的感受,我用图32把这些抽象的数字图表化。可以看到,在图中,代表生日相同的概率的曲线,是随着统计人数的增多而急剧上升的。
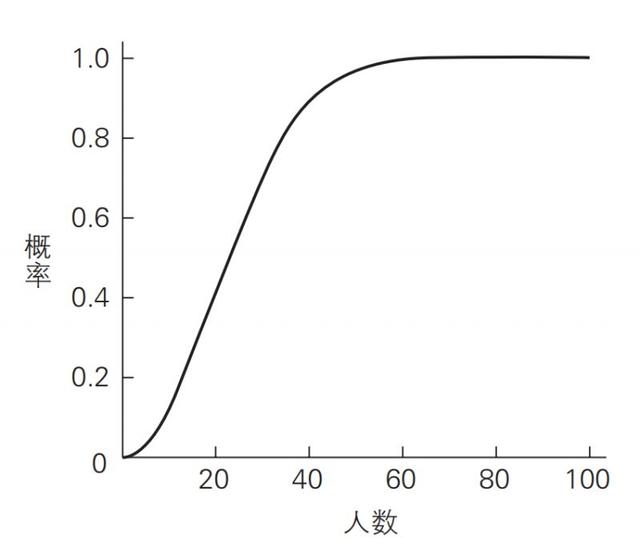
至少有2 人生日相同的概率
上述这种现象被称为“生日悖论”(Birthday Paradox)。我们直觉上认为同一天生日是很少见的事情,但实际上发生的概率却是非常高的。正是因为理性计算的结果与日常经验产生了如此明显的矛盾,该问题才被称为“生日悖论”。
那么,是我们的直觉出错了吗?像“生日悖论”这样实际情况与直觉差异如此之大的现象,又为什么会发生呢?

要解答这个问题,我们需要先去计算一下另外一种特殊情形,那就是在包括自己在内的23 人之中,存在与自己生日相同的人的概率。计算结果显示,这个数字不超过6.1%。只有当样本人数扩大到253 人时,这个概率才有可能会上升到50%。这个结果应该不会令你讶异吧,是不是和你自己心里估算的也差不多呢?
其实,当我们看到“有人生日相同”时,下意识地会用“与我生日相同”去推测,而实际上“与我生日相同”的概率确实非常小。于是,直觉告诉我们,“有人生日相同”的概率也很小。
但是,“生日悖论”中真正的问题其实是23 人中至少有2 人以上生日相同的概率,而不论究竟是谁的生日。这与我们的直觉中预设的前提条件有着根本的不同。
可以说,直觉没有错,错的是我们没有正确地去理解问题。因此,当我们剥开直觉的谎言,看清事实的那一刻,才会觉得如此不可思议。

“同月同日生”的概率
生日悖论中概率的计算,看起来似乎很复杂,但过程其实很简单。
首先,让我们来考虑最简单的情况。假设只有2 个人,如果这2人的生日是同一天,也就是说,都是365 天中的某一天,那么这时生日相同的概率可以计为:1/365
那么,当人数增加到3 个人时呢?第一步要先计算一下这3 个人的生日各不相同的情形有多少对组合,然后用所有可能的组合减去这个数字,就能够得出3 人中至少有2 人生日相同的组合有多少。
3 人生日各不相同时,可以计算得出,一共有如下这么多对组合形式:365*364*363=48228180
而3 人生日中所有可能产生的组合数量是:365**3 = 48627125
那么,我们就可以得出,3 人中至少2 人生日相同的组合数量是:365**3-365*364*363=398945
也就是说,3 人中至少2 人生日相同的概率大约是398945/48627125 = 0.82%。
采用相同的计算方式,我们也可以得出人数为4 人、5 人时,至少有2 人生日相同的概率。而且,计算结果会如图32 中的曲线一样,当人数较少时概率也比较低,当人数稍微有所增加,概率就会像坐了直升机一样迅猛蹿升。
一个人的生日一共有365 种可能,n个人中至少有2人生日相同的概率:
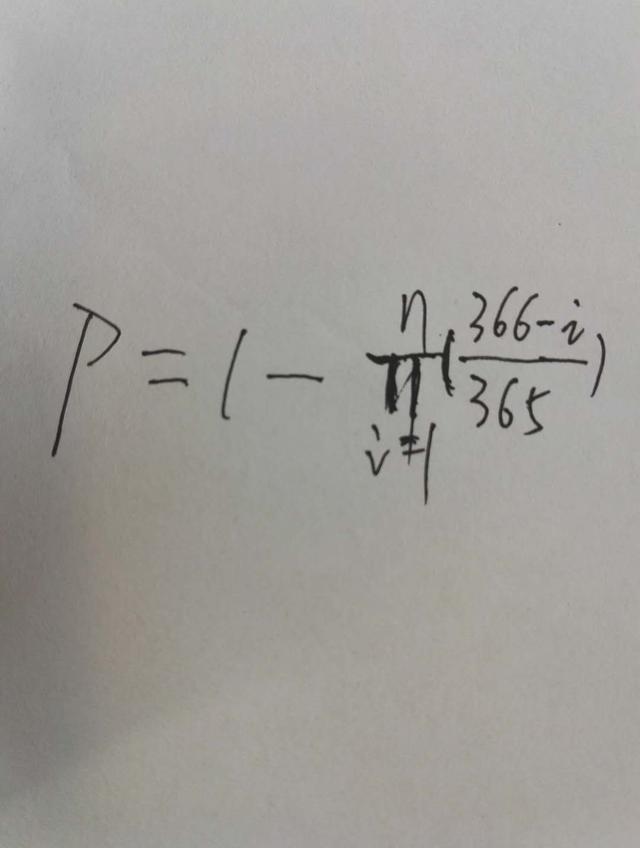
手动计算
我们可以把这个问题写成一般形式,即在有n 种可能的情形下,要使至少有2人生日相同的概率达到50%,则必须p>=50%
需要有如下的样本人数:1.18√n
把365 代入这个公式中,可得:1.18√365 = 22.5
当然,现实中不可能存在22.5 人的情形,但是,这意味着只要样本人数超过这个值,存在相同生日的概率就将超过50%。这个公式证明了,如果样本人数是23 人,那么概率必定超过了50%
这个公式的应用范围非常广,非常方便我们进行类似的计算。比如,我们把“生日”的概念替换为“出生月份”,就同样可以使用这个公式计算出生月份相同的概率。这种情况下,取n = 12(月份数),则1.18√12= 4.1
也就是说,当样本人数大于等于5 时,存在相同出生月份的概率就将超过50%(人数为5 时套用公式计算,实际得到的概率数字超过了60%)。而在现实生活中,我们的第一感觉应该绝不会认为有这么高的概率吧。
这个公式还可以用来计算“月份不同,仅出生日期相同”的概率。
每个月的实际天数有所不同,为方便计算,在这里我们都大致计为30 天,则计算可得:1.18√30= 6.5
也就是说,只要样本人数达到7 个人,存在仅出生日期相同的概率就将超过50%。
除此之外,只要将这个公式稍加变形,其应用范围就将得到延伸。比如计算出生日期虽不一致,但非常接近的情形,如“至少有2 个人出生日期仅间隔1 天的概率”。如果样本人数同样设为23 人,可计算得出这个概率是88.8%。比较一下就会发现,这个数字比起出生日期完全一致的概率要高很多。这就意味着,如果身边某个人和你的生日非常接近,那这件事一点都不稀奇,也并不是什么有缘无缘的问题。