旋转相似是中考的考试的热点,不仅体现在线段的求解,更重要的为解决我们的隐圆及瓜豆模型做了很重的基础支撑,而相似模型作为在相似基本推导的内容里面为数不多的利用两边成比例夹角相等的判定形式。这节内容将对相似进行原理说明。
 原理证明
原理证明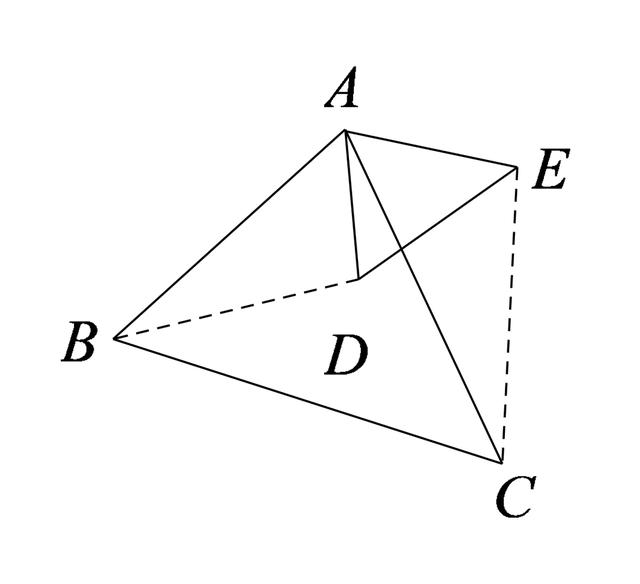
如图,已知△ABC∽△ADE,
则AB/AC=AD/AE,
∠BAC=∠DAE,∴∠BAD=∠CAE,
∴△BAD∽△CAE(SAS)
通过两边成比例夹角相等的判定,
这就是旋转模型的实质。
其次第三边与第三边的夹角等于顶角。
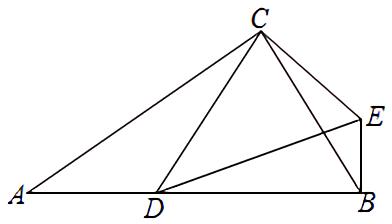
典型例题1.如图,已知△ABC中,∠ACB=90°,点D是边AB上一点,且△CDE∽△CAB
(1)求证:△CAD∽△CBE;
(2)求证:EB⊥AB.
【思路点拨】
(1)根据相似三角形的性质得出两边成比例夹角相等的判定,运用旋转相似的基本模型,进行证明。
(2)由相似之后的八字推角可以推断第三边的夹角等于顶角90°
【解答】
(1)证明:∵△CDE~△CAB,
∴CA/CD=CB/CE,∠ACB=∠DCE
∴∠ACB-∠DCB=∠DCE-∠DCB,
则∠ACD=∠BCE,
∴△CAD∽△CBE;
(2)证明:∵△CAD~△CBE,
∴∠CAD=∠CBE.
∵∠ACB=90°,∠CAD+∠CBA=90°,
∴∠CBE+∠CBA=90°,
∴EB⊥AB.
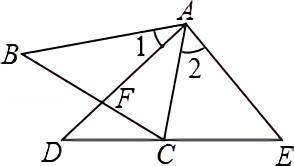
2.如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2,AB/AC=AD/AE
(1)试说明:△ABC∽△ADE;
(2)试说明:AF•DF=BF•CF
【思路点拨】
(1)根据有两组对应边的比相等,且这两边的夹角也相等的两三角形相似旋转相似模型;
(2)根据相似三角形的性质推出∠B=∠D,根据相似三角形的判定推出△ABF∽△CDF,推出比例式,即可得出答案.
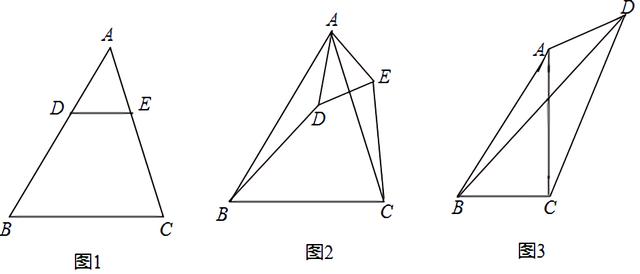
同步练习1.(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=3/2,则BD/CE的值是 ;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD,BD/CE的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=3/4,当CD=6,AD=3时,请直接写出线段BD的长度 .
【解答】
解:
(1)由平行A字相似性质可得答案:4/3
(2)由旋转相似的基本判定
由(1)得:DE∥B,
∴△ADE∽△ABC,
∴AD/AB=AE/AC
由旋转的性质得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴BD/CE=AD/AE=4/3
(3)在AB上截取AM=AD=3,过M作MN∥BC交AC于N,把△AMN绕A逆时针旋转得△ADE,连接CE,如图所示:
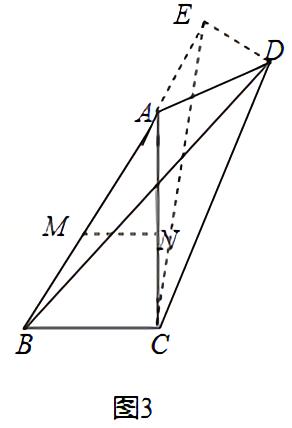
答案:(3√109)/4
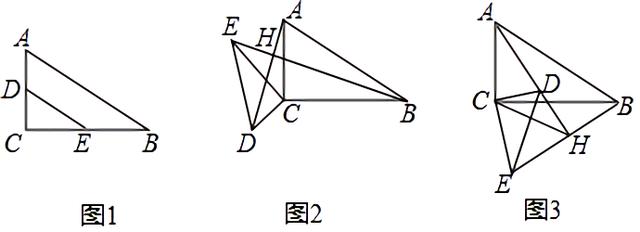
2.已知:已知Rt△ABC中,∠ACB=90°,D、E分别是AC、BC上的点,连DE,且AC/DC=BC/EC=√3,tanB=√2/2,如图1.
(1)如图2,将△CDE绕C点旋转,连AD、BE交于H,求证:AD⊥BE;
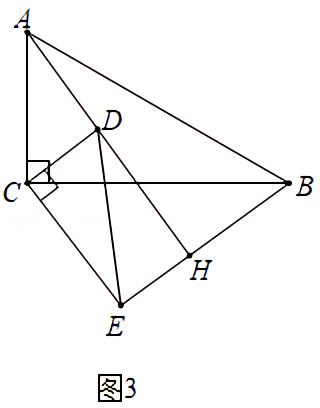
(2)如图3,当△CDE绕C点旋转过程中,当CH=√5时,求√2AH﹣BH的值;
(3)若CD=1,当△CDE绕C点旋转过程中,直接写出AH的最大值是 .
【解答】
(1)证明:如图2中,
由旋转的基本内容判定和性质可以得出对应边成比例夹角相等,可以得出旋转相似。
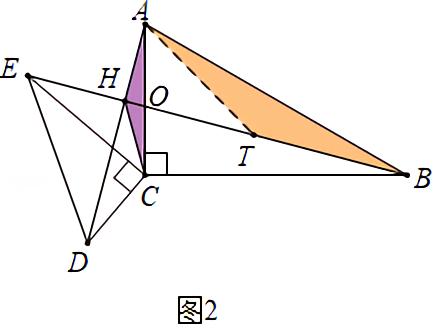
(2)解:由旋转相似的基本内容可以判定线段的比例关系
BT=√15.
(3)解:如图3中,
故答案为:2√2.
姜姜老师点评寄语同学们在学习解答关于相似模型中遇到三角形和四边形问题时候,我们要使用从整体到局部分析的眼光看待问题,虽然看似不难,确是容易出错,思路不清晰的一类题目。相信同学们把这姜姜老师整理的相似模型合集学习完以后再遇到这样的问题就可以迎刃而解。

往期精彩内容:
「中考」初中数学相似模型合集解析16——45°模型讲解
开学啦!忙碌的初三党必看知识点!中考数学相似模型合集15
中考数学相似模型合集解析技巧13、14——一线三等角及变式模型
初中数学相似模型合集解析12——三角形和四边形
初中数学中考重点:相似模型合集9、10——燕尾形模型及勾股型