古代的希腊和中国,很早就发现了无理数。然而东西方却通过不同的途径来认识和发展无理数的理论,从而导致了东西方数学发展的不同方向。希腊人着眼于几何量的长度关系,从线段不可公度的几何角度入手,用逻辑方法进行探讨;中国人着重满足实际应用的数的运算,从开方不尽的计算过程入手,通过计算方式来认识并建立其法则。
一、无理数在古希腊的发现及其影响
公元前500年,古希腊毕达哥拉斯(Pythagoras)学派认为:“万物皆是数”,也就是一切现象都可以用有理数去描述,数学之美在于有理数能解释一切自然现象。“宇宙间的一切现象都归结为整数或整数之比”,在几何上这相当于说:对于任何两条给定的线段,总能找到某第三条线段,以它为单位线段能将给定的两条线段划分为整数段。希腊人称这样两条给定线段为“可公度量”。

毕达哥拉斯学派核心成员
然而,事实并非如此,学派中有人问毕达哥拉斯,边长为1的正方形的对角线,能不能用整数和整数之比来表示呢?这个问题引起了学派成员的讨论,有位学生名叫希帕索斯,出于无聊,他试图找出根号2的等价分数,最终他认识到根本不存在这个分数,也就是说根号2是无理数,希帕索斯对这发现,喜出望外,但是他的老师毕达哥拉斯却非常不高兴,因为毕达哥拉斯已经用有理数解释了天地万物,这个发现动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,无理数的存在会引起信徒们对毕达哥拉斯信念的怀疑,将动摇他和一批领导者在学术界的统治地位。然而,毕达哥拉斯始终不愿承认自己的错误,却又无法经由逻辑推理推翻希帕索斯的论证。使他终身蒙羞的是,他竟然判决将希帕索斯淹死,希帕索斯为真理而献出了宝贵的生命。
由于毕氏学派关于比例定义假定任何两个同类量可通约,比例理论中的所有命题都局限在可通约的量上,因而他们关于相似形的一般理论就失效了。毕氏学派的成员泰奥多勒斯发现,面积等于3、5、6、17 …的正方形的边与单位正方形的边也不可通约,并对每一种情况都单独予以证明。希腊数学中出现的这一逻辑困难,被称为数学史上的“第一次数学危机”。危机的解决大约在公元前370年,才华横溢的希腊数学家毕达哥拉斯的学生阿契塔和欧多克索斯以及柏拉图给出两个相等的定义从而消除了这次危机。
这次危机使人们认识到直观、经验乃至实验都不是绝对可靠的(例如用任何实验都不能得出一切量均可用有理数表示这个结果),今后必须依靠证明用理性思维思考自然界。此外,它使古希腊数学研究的重点由算术转向几何,打破了在这之前毕达哥拉斯学派把数和几何问题等同起来的看法,即几何学的某些真理与算术无关,几何量不能完全由整数及整数的比来表示,反之数却可以由几何量表示出来,可以说这次发现对古希腊的数学观点有极大的冲击,整数的尊崇地位受到了挑战。而且这次危机使古希腊数学研究方法由计算转向推理,促使公理方法的产生,从此希腊人开始由“自明的”公理出发,经过演绎推理而建立起几何学体系。
二、无理数在中国的发现及其影响
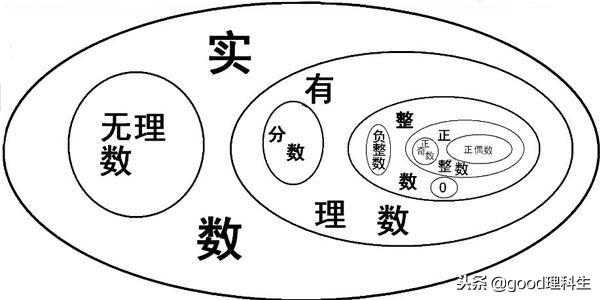
中国古代在处理开方问题时,不可避免地碰到了无理根数。中国早期的开方术见于刘徽的《九章算术》少广、勾股两章,起源于长度的测度。已知面积求正方形边长;已知体积求立方体棱长;已知圆面积求圆的直径;已知球体积求球的直径或直角三角形勾、股、弦互求。

《九章算术》“少广”章的开(平)方术有“若开之不尽者,为不可开,当以面命之”,“令不加借算而命分,则常微少;其加借算而命分,则又微多。其数不可得而定。……故惟以面命之,为不失耳”,这说明刘徽认识到“加不加借算命分”都得到的不是精确值,只有用被开方数的方根表示才是精确的,接着他在“开方术注”中提出一种更为精确的表示方根近似值的方法,即求微数法:“不以面命之,加定法如前,求其微数。微数无名者以为分子,其一退以十为母,其二退以百为母。退之弥下,其分弥细,则朱幂虽有所弃之数,不足言之”,就是用10进制小数来无限逼近无理数。中算学家没有像希腊人那样在发现无理数时出现逻辑上的困难,又能顺利地将有理数运算规则推广到无理数,因此把数学向前推进的同时,并没有深究无理数与有理数实质上的不同。
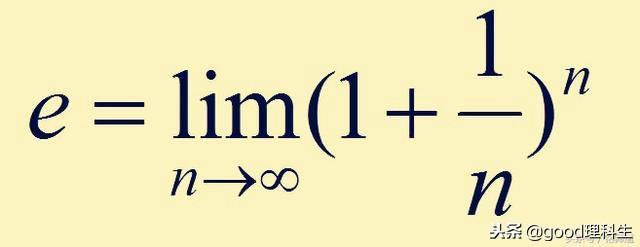
由于并没有经历过西方的数学危机革命,中国的数学仍停留在“算术”阶段,在筹算开平方和开立方的基础上,我国从11 世纪开始,逐渐摸索到数值解高次方程的一般规律。北宋数学家贾宪,在前人的基础上,发明了开任意高次幂的“增乘开方法”,它是我国古代数学史上一项杰出创造,是一个非常有效和高度机械化的算法,公元1819年英国数学家霍纳才得出同样的算法。贾宪的“增乘开方法”不仅适用于开任意高次方,而且能得出高次方程的数值解法。经过200多年的不断改善,到13世纪上半叶,由秦九韶最后完成完整的体系——秦九韶求实根法,即解高次方程的“正负开方术”。其方程的各系数可正可负,可以是整数或小数,开方得到无理根时,秦九韶发挥了刘徵首创的计算“微数”的思想,用十进小数作无理根的近似值。这一时期,数学人才辈出,有北宋的沈括、贾宪和刘益;南宋的秦九韶、杨辉;元代的李冶、朱世杰、郭守敬等,使宋元时期的数学达到了中国古代数学的顶峰,尤其在代数领域达到了西方望尘莫及的水平。
三、东西方数学的比较与分析
由此可以看到第一次数学危机后,东方和西方的数学走向了两个不同方向,那么这种差异的产生究竟是因为什么呢?首先,东方中国的古代文化的经济基础基本上是农业经济。因此中国古代数学也与农业经济有着密切的关系。《九章算术》所记载的问题大都与农业生产有关,用来解决农田的测量、粟米的称量,农业水利工程的测算等。这种自给自足的自然经济的生产力状况决定的生产力关系是以家族为中心、以血缘关系为纽带的宗法等级关系,社会制度是宗法等级制度。在这种社会制度的影响和作用下,形成中国古代稳定的上下尊卑等级秩序的文化心理。主要特点是静态的、和解的、自然的、消极的心理特点。造成安于现状的生活方式、工作方式、管理方式。另一方面,汉王朝建立以后的“重农抑商”政策使数学研究受不到贸易的诱惑。农业经济的财富有限和填饱肚子的生活状况,不允许人们的思想向实用以外的地方延伸;隋朝开始的科举制度也扼杀了大批在数学研究上具有不凡才华的人。这些都导致了中国古代数学过于注重于实际的传统从而限制了对理论问题作更深层次的探讨,因而也阻碍了无理数的发现,使得中国古代数学的许多成就只处在应用和描述过程阶段,没有提高到抽象的、系统的理论阶段,从而使数学的发展和升华受到限制。

刘徽
此外,未发现无理数还与刘徽“一者数之母”的观念有密切关系。“一者数之母”的主张,不是从来就有的。中国古代广泛存在着“一以统众”的思想,如《管子·轻重》提出“天下之数,尽于轻重”,把古代统治者所推行的政治和经济措施,全用“轻重”二字统御起来;而道论更是把一切都置于“道”的统领之下,至王弼他一方面说“演天地之数,所赖者五十。其用四十有九,其一不用也;不用而用以通之,非数而数以之成,即易之太极也”,认为“一”是统一包括数在内的一切的“太极”而“一”本身不是数;一方面又说“一,数之始而物之极也”,“一,少之极也”,虽然这里已隐约含有“一为万物之母”,而且“一”也可以是数的思想,但这是一种非常模糊的观念。刘徽在这种“一以统众”的思想氛围之下,从前人的思想和自己的数学实践中提炼和升华出“一者数之母”的原理来,这条原理,一旦在他的工作中得到大量的验证,而没有遇到什么困难,是很难想到要怀疑它的。中国古代数学以实用为目的的传统,大大削弱了探求理论基础的动力,而“一者数之母”作为古代数学的原理,正好消除了达到其目的时可能出现的顾忌,而从整个中国数学史的发展角度看,可以认为它某种程度上阻碍了无理数的发现。

希腊爱琴海
而在西方,小亚西亚海岸新兴的商业城市、希腊本土、西西里岛和意大利海滨,由于海上贸易和战争的刺激使得人们的思想活跃,商品贸易发达,对计算要求的提高,财富的增加使人们有更多的时间从事“非实用”的理论研究,从而形成了著名的七大学派。他们是先后在爱奥尼亚地区的泰勒斯学派,毕达哥拉斯学派、厄里亚学派、巧辩学派和在雅典地区的柏拉图学派、欧多克索学派、亚里士多德学派。他们不仅是数学家还大都是哲学家,他们思想深邃,以探索自然奥秘为目的进行数学研究或者指导数学研究。这些哲学家和科学家们把数学从以往的经验形态上升为理论形态,为后来数学的发展奠定了基础。与古代东方静态的观点不一样,人们不但要知其“然”,而且要知其“所以然”。不但要问“什么”,而且要问“为什么”,要解决“所以然”和“为什么”。亚里士多德的名言“吾爱吾师,吾更爱真理”就是对这一观点的有力体现,也正因为如此希帕索斯才会坚持自己的理论并将之公布于众,由此引发了第一次数学危机。为了知道“所以然”和 “为什么”,就得在数学的证明方法上作一定的努力,在这样的文化氛围中现代意义上的数学产生了。此外不同于东方的重农抑商,西方的商业贸易的兴起与发达、财富的增长,使得人们旅行的欲望越来越高,而旅行和游动的生活方式也给数学的进一步发展提供了机遇。