以不变应万变,活用思维定势——2019年湖北武汉中考数学第23题

思维定势,换个说法也叫思维习惯,在解题过程中,有时它会起到导引思维的作用,有时也会因此固化思维,所以它既非褒义也非贬义。我们在八年级学习三角形全等以及九年级学习相似时,便接触到一些基本的全等案例,它们源于课本例题和习题,如果把它们用活了,在解几何压轴题时,往往会有意想不到的好处。
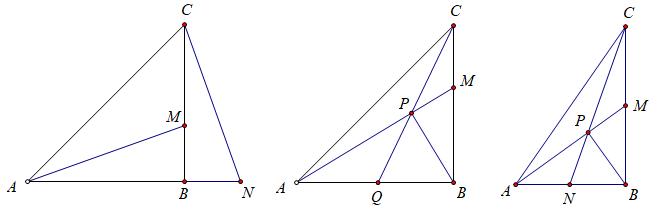
题目
在△ABC中,∠ABC=90°,AB:BC=n,M是BC上一点,连接AM
(1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN;
(2)过点B作BP⊥AM,P为垂足,连接CP并延长交AB于Q
①如图2,若n=1,求证:CP:PQ=BM:BQ
②如图3,若M是BC中点,直接写出tan∠BPQ的值(用含n的式子表示)
解析
(1)如果是八年级学生刚刚学完全等三角形的判定,看这道题会感觉无比亲切,当n=1时,AB=BC,再加上∠ABM=∠CBN=90°,全等二缺一,考虑到AM与CN的垂直关系,只需要延长AM交CN于点D,便可完成剩下条件的证明,如下图:
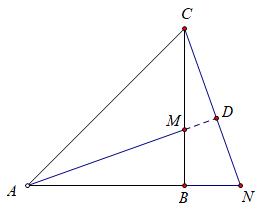
很容易得到△ABM≌△CBN,于是BM=BN;
(2)前一小题的全等三角形,在恰好时机,能让它们重现,当然,略有区别。
①依然有n=1,因此仍然会有AB=BC,不妨将前一小题中的全等三角形构造出来,用不同的思路,延长AB至N,使BN=BM,连接CN,延长AM交CN于点D,怎么样?熟悉的图形又回来了吧?
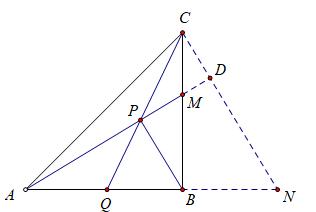
根据辅助线作法,BM=BN,再加上AB=BC,∠ABM=∠CBN=90°,于是仍然可证△ABM≌△CBN,所以∠BAM=∠BCN,而∠BCN+∠N=90°,所以∠BAM+∠N=90°,从而可以证明AD⊥CN,看看能发现什么?
根据BP⊥AM,我们可得到BP∥CN,本小题求证的结论是一个比例式,而此时居然出现了平行线,正好可采用平行线分线段成比例定理,得到CP:PQ=BN:BQ,最后将其中的BN换成BM即可,得到CP:PQ=BM:BQ;
②在尝到了甜头之后,最后一小题中,是否也能采用以上的基本方法呢?n≠1,大不了将前面的全等换成相似嘛!
而求三角函数值,最佳途径是构造直角三角形,注意到BP⊥AM这个条件,结合M点是中点,不妨用倍长中线法,延长PM至点D,使PM=DM,连接CD并延长,交AB延长线于点N,如下图:
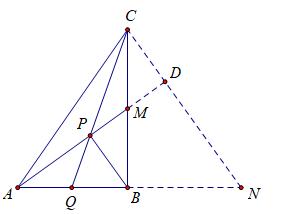
既然采用倍长中线法,那么首先便可得到△BPM≌△CDM,所以∠CDM=∠BPM=90°,我们再一次得到BP∥CN,∠BPQ=∠DCP,而同时求三角函数所需要的直角三角形也构造成功,是Rt△CDP,我们只需要表示出DP和CD的长即可。
观察图中的所有直角三角形,我们可发现,Rt△ABM、Rt△CBN、Rt△DCM均彼此相似,我们只需要利用好它们之间的比例关系,由Rt△ABM∽Rt△CBN,我们可以得到AB:BC=BM:BN=n,不妨设BC=x,于是AB=nx,而BM=x/2,所以可表示出BN=x/2n,在Rt△CBN中,利用勾股定理表示出CN,再来推导CD和DP的长,如下图:
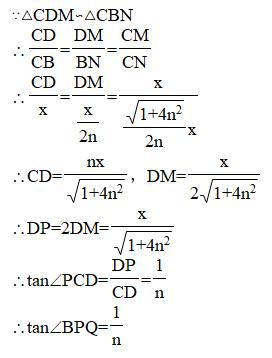
解题反思
从第一小题的全等,到第二小题的全等,再到第三小题的相似,全部是基本图形,全部是常规方法,解完后再回过头看这三幅图的辅助线,仿佛一个模子出来,正所谓以不变应万变。而思维惯势,在这道压轴题的解题过程中,成为了助力。旋转90°的两个直角三角形,八字形三角形,倍长中线法,平行线分线段成比例,在直角三角形中求三角函数值,勾股定理,相似比一定的相似三角形等常规常法,以一种非常和谐的形式融合到了一起。看上去,和课本例题差不多,实际上也差不多,第一次构造出全等三角形和第二次构造,证明方法不同,前面的条件在后一小题中成为结论,这些对学生的深入理解能力提出了较高要求。
都是基本功,但内功深厚,使将出来,威力自然不可同日而语。
微信公众号:爱数学做数学