初中数学,几何证明辅助线技巧方法。通过这些类型,基本可以学会包括初中辅助线大多数技巧方法。所有题目都是作者自己选题,自己画图,而且每道题都有视频讲解。
1、平移法,当一个图形有两条相等线段相交,其夹角为特殊角时,一般都是平移。或者两条关联线段需要转化通用三角形时,也可以用平移法。初中范围内关于这类题不是很多,大约掌握十题左右就差不多了。分类刷题,总结方法,举一反三,学习努力很重要,但怎么学更加重要。
2、面积法解题,一般这样的题的特征都是两个以上的直角。可以用面积法找到等量关系,也称为等积法。这样的题在初中范围内出现的不多,典型的也就不超过十题,而且还是互相变化得到的。所以只要掌握很少的几题,这类面积问题就可以过关了。下面给出的是比较典型的模型常考题,同学们可以参考一下。
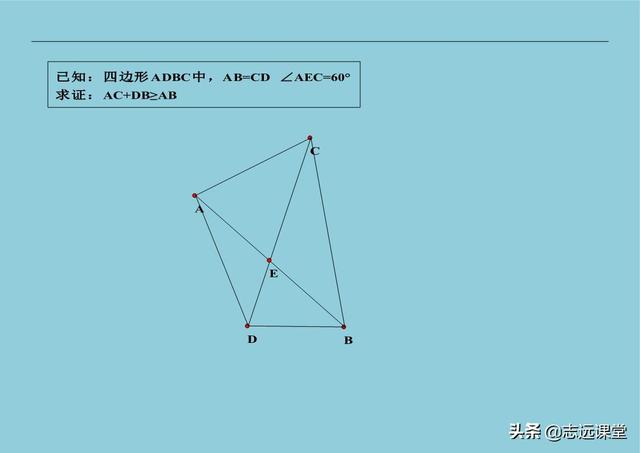
3、八字证明线段大小关系,大家都知道八字倒角法,其实八字还有一个结论就是线段大小关系。结论就是交叉两条线段之和大于另外两条线段之和。所依靠的知识点是,三角形两边之和大于第三边,有了这样的提示此结论不难证明。然后运用此结论解决下面这道例题,我们平时做题不要为了完成答案而做题,更应该去想这一类题的特征以及解决方法。
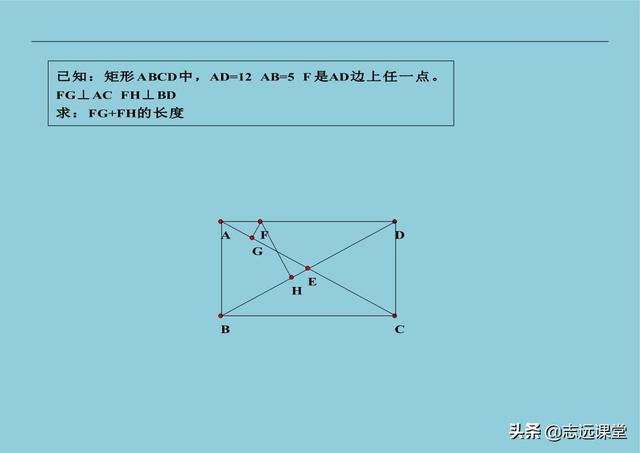
4、四边形中点辅助线,遇到有四边形(平行四边形、矩形、菱形、正方形)有边中点。一般都是中点处的线段进行延长,可以得到八字全等图形。因为平行和中点组合,就是构造八字全等图形的特征。下面的习题大家可以按照这个解题思路试一下,以后遇到类似已知就能做到举一反三的效果。
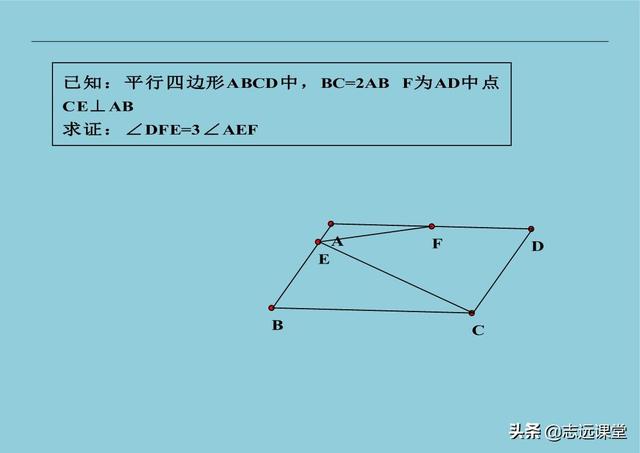
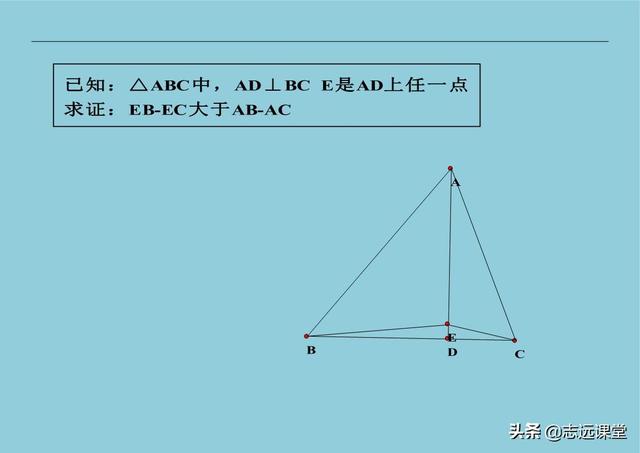
5、手拉手模型(也叫子母图、哥俩好、初中第一图、神图等),两个一大一小两个相似图形共顶点。常见的是两个等边三角形、两个等腰直角三角形、两个正方形等。这个图形常见结论就是出全等,而由全等可以扩展出十几个其它结论,大约一年前我曾经发过这十几个结论。而且这个图形还和其它一些模型有联系,比如费马点、托勒密定理等。由此基本图形扩展出的中考题不计其数,记得十年前,我教过的一位同学,把这个图和结论挂在墙上。同时幸运的是,那一年中考就是手拉手的变形,哪个时候还没有出现手拉手这个名字,我称这个模型叫初中第一图,现在某网站上还有我录的视频讲解。可是现在,十年过去了,这个模型已经被玩坏了,被老师们研究的太透彻,好多省市已经不敢考这个图形了。
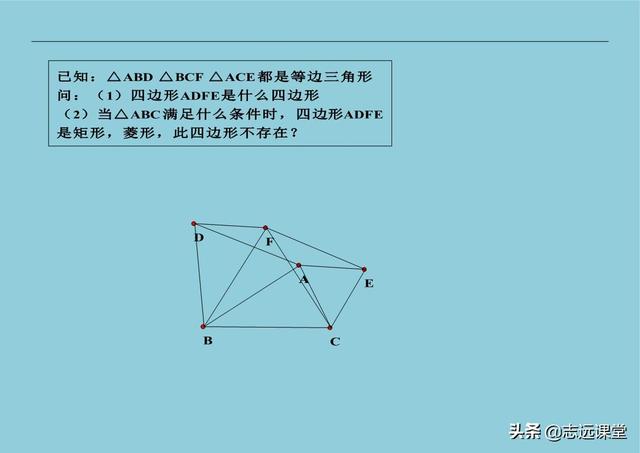
6、等腰三角形(包括等边)常用辅助线。做三线合一; 做一边的平行线,出小等腰; 延长一腰至等长,连接后出直角三角形; 等腰外面扩等边,连接两顶点出30度角。
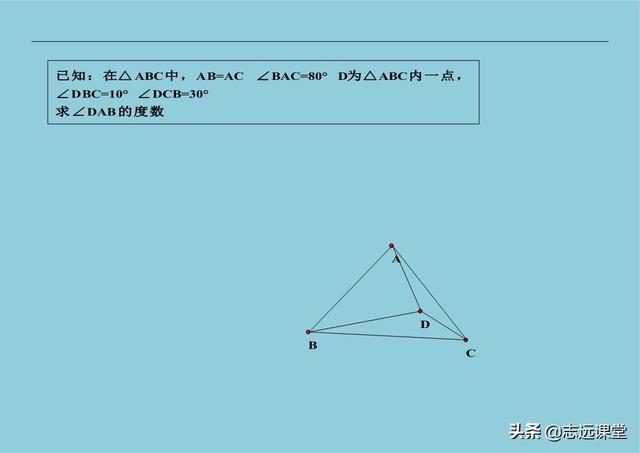
7、等腰直角三角形常用辅助线,两直角边处构造全等。因为等腰直角三角形有相等的边,而直角又很容易为全等角相等创造条件,而且等边三角形和正方形有时候也符合这个规律。这个方法出自教材中的“赵爽弦图”,无论是三垂直模型,还是其它类似问题。
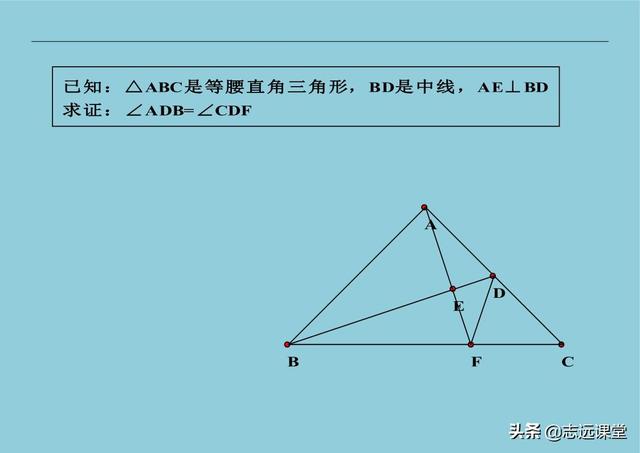
8、初中有一种不常考的类型,藏角题。一般这类题都是利用线段之间的数量关系,产生特殊角度。没刷过这类问题的同学,确实有一定难度。大家可以参考下面习题,研究一下这类问题,注意不是会做就可以了,而是探索这类题的特征与方法。特别是教学人员,会做题只是教学的初级层次,研究教法、教会不同层次的学生才是重要的,别跑偏了!
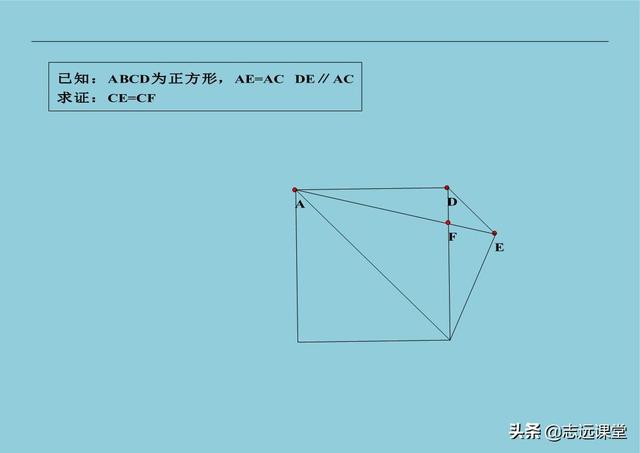
9、旋转辅助线特征:已知中有相等的线段共顶点; 对角之和180°; 半角模型是旋转; 费马点是旋转; 手拉手(哥俩好、子母图、初中第一图)模型是旋转,还有其他特征可供学习。
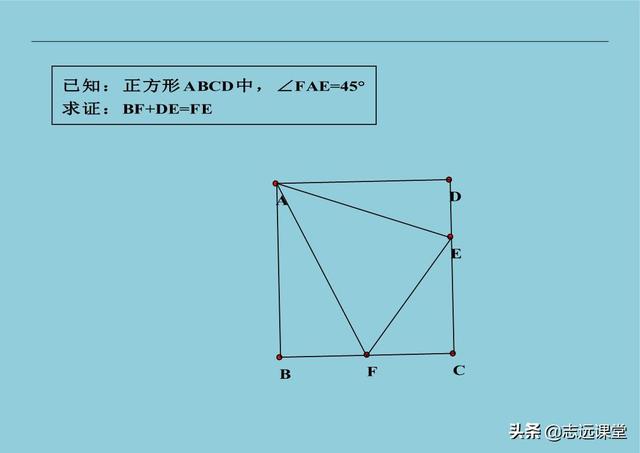
10、直角三角形中点辅助线:有斜边中点连斜边中线; 有斜边倍分关系时,做斜边中线或延长至等长。 就上面两句辅助线总结,无论学生还是老师,都有参考价值。
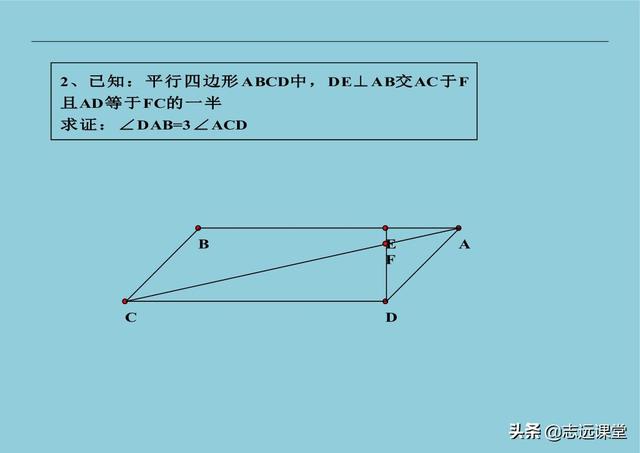
11、角平分线截取证全等:已知中有角平分线,在长边上截取线段等于短边,截取的点与角平分线上某一点相连,出全等。当然,如果延长也可以,这就是老师常说的截长补短。这才是真正的教方法技巧,简单直接,一看就懂!
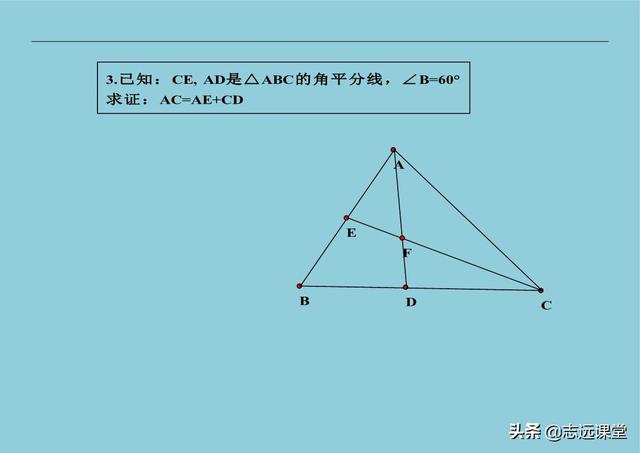
12、角平分线延长出全等:已知中被平分的角一边上有一点,向角平分线有垂直线段,一般都是延长与另一边或其延长线相交,出全等。看懂这句话,你就又学会了一种辅助线做法,价值比上一次一对一都要高,用这种方法,解决一下下面的习题吧!
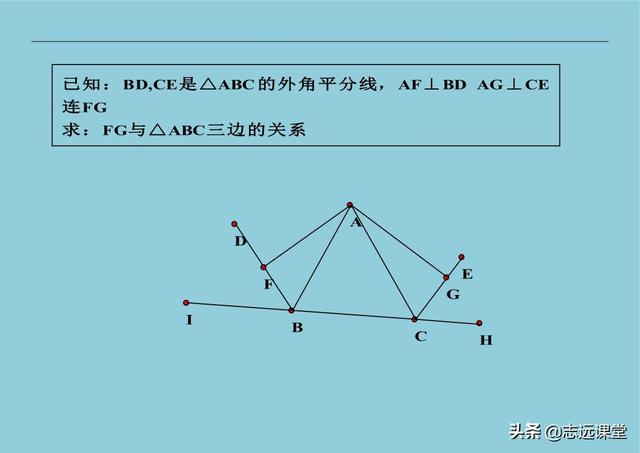
13、已知中出现两个中点:一般都是在某边上再找一中点,与已知两中点相连,构造两个中位线。这是比较常用的辅助线技巧方法,仔细体会一下吧!用这么少的语言告诉您方法,一定是干货。
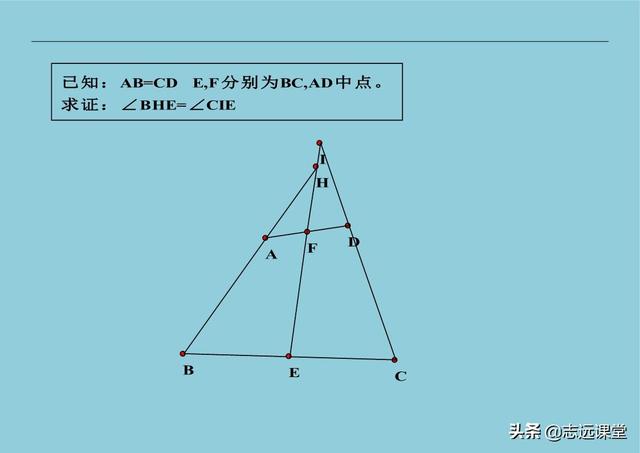
14、一个中点如何做辅助线,构造八字全等。一般都是倍长相等的线段,出现全等三角形,而且还有平行的线段。
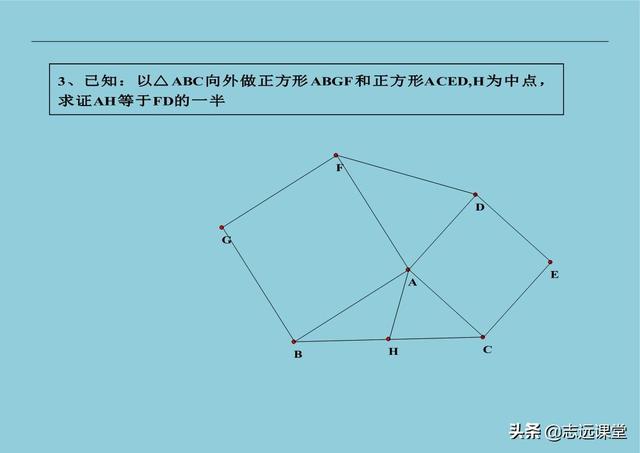
上面所总结的,是初中数学几何辅助线文字记忆版。所有方法为志远老师总结,此文章可以不作为商业用途,随意使用。